So finden Sie Projektionen eines Vektors auf Koordinatenachsen. Vektoren und Operationen auf Vektoren. Vektorprojektionseigenschaften
Definition 1. Auf einer Ebene ist eine Parallelprojektion von Punkt A auf die l-Achse ein Punkt – der Schnittpunkt der l-Achse mit einer geraden Linie, die durch Punkt A parallel zu dem Vektor gezogen wird, der die Entwurfsrichtung angibt.
Definition 2. Die Parallelprojektion eines Vektors auf die l-Achse (zum Vektor) ist die Koordinate des Vektors relativ zur Basis Achse l, wobei die Punkte und parallele Projektionen der Punkte A und B auf die l-Achse sind (Abb. 1).
Nach der Definition, die wir haben
Definition 3. wenn und l-Achsen-Basis Kartesisch, also die Projektion des Vektors auf die l-Achse genannt orthogonal (Abb. 2).
Im Raum bleibt die Definition 2 der Vektorprojektion auf die Achse bestehen, lediglich die Projektionsrichtung wird durch zwei nicht kollineare Vektoren angegeben (Abb. 3).

Aus der Definition der Projektion eines Vektors auf eine Achse folgt, dass jede Koordinate eines Vektors eine Projektion dieses Vektors auf die durch den entsprechenden Basisvektor definierte Achse ist. In diesem Fall wird die Entwurfsrichtung durch zwei weitere Basisvektoren angegeben, wenn der Entwurf im Raum ausgeführt (betrachtet) wird, oder durch einen anderen Basisvektor, wenn der Entwurf in einer Ebene betrachtet wird (Abb. 4).

Satz 1. Die orthogonale Projektion eines Vektors auf die l-Achse ist gleich dem Produkt aus dem Modul des Vektors und dem Kosinus des Winkels zwischen der positiven Richtung der l-Achse und, d. h.

Andererseits
Von uns finden
Wenn wir AC in die Gleichung (2) einsetzen, erhalten wir
Da die Zahlen X und das gleiche Vorzeichen in beiden betrachteten Fällen ((Abb. 5, a) ; (Abb. 5, b), dann folgt aus Gleichheit (4).
Kommentar. Im Folgenden betrachten wir nur die orthogonale Projektion des Vektors auf die Achse und verzichten daher in der Notation auf das Wort „ort“ (orthogonal).
Lassen Sie uns eine Reihe von Formeln vorstellen, die später bei der Lösung von Problemen verwendet werden.
a) Projektion des Vektors auf die Achse.
Wenn ja, dann hat die orthogonale Projektion auf den Vektor gemäß Formel (5) die Form
c) Abstand von einem Punkt zu einer Ebene.

Sei b eine gegebene Ebene mit einem Normalenvektor, M ein gegebener Punkt,
d ist der Abstand vom Punkt M zur Ebene b (Abb. 6).
Wenn N ein beliebiger Punkt der Ebene b ist und und Projektionen der Punkte M und N auf die Achse sind, dann
- G) Der Abstand zwischen sich schneidenden Linien.

Es seien a und b gegebene sich kreuzende Linien, ein zu ihnen senkrechter Vektor, A und B beliebige Punkte der Linien a bzw. b (Abb. 7) und und dann Projektionen der Punkte A und B auf sie
e) Abstand von einem Punkt zu einer Linie.
Lassen l- eine gegebene Gerade mit einem Richtungsvektor, M - ein gegebener Punkt,
N – seine Projektion auf die Linie l, dann - der erforderliche Abstand (Abb. 8).
Wenn A ein beliebiger Punkt auf einer Geraden ist l, dann können in einem rechtwinkligen Dreieck MNA die Hypotenuse MA und die Beine gefunden werden. Bedeutet,

f) Der Winkel zwischen einer Geraden und einer Ebene.

Sei der Richtungsvektor dieser Linie l, - Normalenvektor einer gegebenen Ebene b, - Projektion einer Geraden l zur Ebene b (Abb. 9).
Bekanntlich ist der Winkel μ zwischen einer Geraden l und seine Projektion auf die Ebene b wird Winkel zwischen der Geraden und der Ebene genannt. Wir haben
Lassen Sie uns Beispiele für die Lösung metrischer Probleme mit der Vektorkoordinatenmethode geben.
Erinnern wir uns zunächst daran, was es ist Koordinatenachse, Projektion eines Punktes auf eine Achse Und Koordinaten eines Punktes auf der Achse.
Koordinatenachse- Dies ist eine gerade Linie, der eine Richtung gegeben ist. Man kann es sich als einen Vektor mit einem unendlich großen Modul vorstellen.
Koordinatenachse gekennzeichnet durch einen Buchstaben: X, Y, Z, s, t... Normalerweise wird (willkürlich) ein Punkt auf der Achse ausgewählt, der als Ursprung bezeichnet und in der Regel mit dem Buchstaben O bezeichnet wird Entfernungen zu anderen für uns interessanten Punkten werden gemessen.
Projektion eines Punktes auf eine Achse- Dies ist die Basis der Senkrechten, die von diesem Punkt zu dieser Achse abgesenkt wird (Abb. 8). Das heißt, die Projektion eines Punktes auf die Achse ist ein Punkt.
Punktkoordinate auf der Achse- Das ist die Nummer Absolutwert Dies ist gleich der Länge des Achsensegments (im ausgewählten Maßstab), das zwischen dem Ursprung der Achse und der Projektion des Punktes auf diese Achse eingeschlossen ist. Diese Zahl wird mit einem Pluszeichen angegeben, wenn die Projektion des Punktes in Richtung der Achse von ihrem Ursprung aus liegt, und mit einem Minuszeichen, wenn sie in der entgegengesetzten Richtung liegt.
Skalare Projektion eines Vektors auf eine Achse- Das Nummer, dessen absoluter Wert gleich der Länge des Achsensegments (im ausgewählten Maßstab) ist, das zwischen den Projektionen des Startpunkts und des Endpunkts des Vektors eingeschlossen ist. Wichtig! Normalerweise anstelle des Ausdrucks Skalare Projektion eines Vektors auf eine Achse sie sagen einfach - Projektion des Vektors auf die Achse, das heißt das Wort Skalar abgesenkt. Vektorprojektion wird mit demselben Buchstaben wie der projizierte Vektor bezeichnet (in normaler, nicht fetter Schrift), mit einem niedrigeren (in der Regel) Index des Namens der Achse, auf die dieser Vektor projiziert wird. Wenn beispielsweise ein Vektor auf die X-Achse projiziert wird A, dann wird seine Projektion mit a x bezeichnet. Wenn derselbe Vektor auf eine andere Achse, beispielsweise die Y-Achse, projiziert wird, wird seine Projektion mit a y bezeichnet (Abb. 9).

Berechnen Vektorprojektion auf die Achse(zum Beispiel die X-Achse) ist es notwendig, die Koordinate des Startpunkts von der Koordinate seines Endpunkts zu subtrahieren
a x = x k − x n.
Wir müssen uns daran erinnern: Die Skalarprojektion eines Vektors auf eine Achse (oder einfach die Projektion eines Vektors auf eine Achse) ist eine Zahl (kein Vektor)! Darüber hinaus kann die Projektion positiv sein, wenn der Wert x k größer als der Wert x n ist, negativ, wenn der Wert x k kleiner als der Wert x n ist, und gleich Null, wenn x k gleich x n ist (Abb. 10).

Die Projektion eines Vektors auf eine Achse kann auch ermittelt werden, indem man den Modul des Vektors und den Winkel kennt, den er mit dieser Achse bildet.
Aus Abbildung 11 geht hervor, dass a x = a Cos α
Das heißt, die Projektion des Vektors auf die Achse ist gleich dem Produkt aus dem Modul des Vektors und dem Kosinus des Winkels zwischen Achsenrichtung und Vektorrichtung. Wenn der Winkel spitz ist, dann ist Cos α > 0 und a x > 0, und wenn er stumpf ist, dann ist der Kosinus des stumpfen Winkels negativ und die Projektion des Vektors auf die Achse ist ebenfalls negativ.

Winkel, die von der Achse gegen den Uhrzeigersinn gemessen werden, gelten als positiv, und Winkel, die entlang der Achse gemessen werden, sind negativ. Da der Kosinus jedoch eine gerade Funktion ist, also Cos α = Cos (− α), können Winkel bei der Berechnung von Projektionen sowohl im Uhrzeigersinn als auch gegen den Uhrzeigersinn gezählt werden.
Bei der Lösung von Problemen werden häufig die folgenden Eigenschaften von Projektionen verwendet: if
A = B + C +…+ D, dann a x = b x + c x +…+ d x (ähnlich wie bei anderen Achsen),
A= m B, dann a x = mb x (ähnlich für andere Achsen).
Die Formel a x = a Cos α lautet sehr oft Beim Lösen von Problemen treten Fehler auf, die Sie unbedingt kennen müssen. Sie müssen die Regel zur Bestimmung der Projektion kennen auswendig!
Erinnern!
Um die Projektion eines Vektors auf eine Achse zu ermitteln, muss der Modul dieses Vektors mit dem Kosinus des Winkels zwischen der Richtung der Achse und der Richtung des Vektors multipliziert werden.
Noch einmal – auswendig!
Einleitung………………………………………………………………………………3
1. Wert von Vektor und Skalar…………………………………….4
2. Definition von Projektion, Achse und Koordinate eines Punktes………………...5
3. Projektion des Vektors auf die Achse………………………………………………………...6
4. Grundformel der Vektoralgebra……………………………..8
5. Berechnung des Moduls eines Vektors aus seinen Projektionen…………………...9
Fazit……………………………………………………………………………...11
Literatur……………………………………………………………………………...12
Einführung:
Die Physik ist untrennbar mit der Mathematik verbunden. Die Mathematik gibt der Physik die Mittel und Techniken an die Hand, um die Beziehung zwischen physikalischen Größen, die als Ergebnis experimenteller oder theoretischer Forschung entdeckt werden, allgemein und präzise auszudrücken. Schließlich ist die experimentelle Forschungsmethode die wichtigste. Das bedeutet, dass ein Wissenschaftler Berechnungen anhand von Messungen offenlegt. Bezeichnet die Beziehung zwischen verschiedenen physikalischen Größen. Dann wird alles in die Sprache der Mathematik übersetzt. Gebildet mathematisches Modell. Physik ist eine Wissenschaft, die die einfachsten und zugleich allgemeinsten Gesetze untersucht. Die Aufgabe der Physik besteht darin, in unseren Köpfen ein Bild der physikalischen Welt zu schaffen, das ihre Eigenschaften am besten widerspiegelt und solche Beziehungen zwischen den Elementen des Modells gewährleistet, die zwischen den Elementen bestehen.
Die Physik erstellt also ein Modell der Welt um uns herum und untersucht ihre Eigenschaften. Aber jedes Modell ist begrenzt. Bei der Modellierung eines bestimmten Phänomens werden nur Eigenschaften und Zusammenhänge berücksichtigt, die für ein bestimmtes Phänomenspektrum wesentlich sind. Das ist die Kunst eines Wissenschaftlers – aus der Vielfalt das Wesentliche auszuwählen.
Physikalische Modelle sind mathematisch, aber Mathematik ist nicht ihre Grundlage. Quantitative Beziehungen zwischen physikalischen Größen werden durch Messungen, Beobachtungen usw. ermittelt experimentelle Forschung und werden nur in der Sprache der Mathematik ausgedrückt. Es gibt jedoch keine andere Sprache für die Konstruktion physikalischer Theorien.
1. Bedeutung von Vektor und Skalar.
In der Physik und Mathematik ist ein Vektor eine Größe, die durch ihren Zahlenwert und ihre Richtung charakterisiert wird. In der Physik gibt es viele wichtige Größen, die Vektoren sind, zum Beispiel Kraft, Position, Geschwindigkeit, Beschleunigung, Drehmoment, Impuls, elektrische und magnetische Feldstärke. Sie können anderen Größen wie Masse, Volumen, Druck, Temperatur und Dichte gegenübergestellt werden, die durch eine gewöhnliche Zahl beschrieben werden können, und werden als „ Skalare".
Sie werden entweder in normalen Buchstaben oder in Zahlen (a, b, t, G, 5, −7...) geschrieben. Skalare Größen können positiv oder negativ sein. Gleichzeitig können einige Untersuchungsobjekte solche Eigenschaften haben Gesamte Beschreibung Für den Fall, dass sich die Kenntnis nur eines numerischen Maßes als unzureichend erweist, ist es auch erforderlich, diese Eigenschaften durch die Richtung im Raum zu charakterisieren. Solche Eigenschaften werden durch Vektorgrößen (Vektoren) charakterisiert. Vektoren werden im Gegensatz zu Skalaren durch fette Buchstaben gekennzeichnet: a, b, g, F, C....
Oft wird ein Vektor durch einen Buchstaben in normaler (nicht fetter) Schriftart gekennzeichnet, über dem sich jedoch ein Pfeil befindet:
Darüber hinaus wird ein Vektor häufig durch ein Buchstabenpaar (normalerweise in Großbuchstaben) bezeichnet, wobei der erste Buchstabe den Anfang des Vektors und der zweite das Ende angibt.
Der Modul eines Vektors, also die Länge eines gerichteten Geradensegments, wird mit denselben Buchstaben wie der Vektor selbst bezeichnet, jedoch in normaler (nicht fetter) Schrift und ohne darüber liegenden Pfeil oder auf genau die gleiche Weise als Vektor (d. h. fett oder normal, aber mit Pfeil), aber dann ist die Vektorbezeichnung in vertikale Striche eingeschlossen.
Ein Vektor ist ein komplexes Objekt, das gleichzeitig durch Größe und Richtung gekennzeichnet ist.
Es gibt auch keine positiven und negativen Vektoren. Aber Vektoren können einander gleich sein. Dies ist beispielsweise der Fall, wenn a und b die gleichen Module haben und in die gleiche Richtung gerichtet sind. In diesem Fall ist die Notation wahr A= b. Es ist auch zu bedenken, dass dem Vektorsymbol ein Minuszeichen vorangestellt sein kann, zum Beispiel -c. Dieses Zeichen zeigt jedoch symbolisch an, dass der Vektor -c den gleichen Modul wie der Vektor c hat, aber in die entgegengesetzte Richtung gerichtet ist Richtung.
Der Vektor -c wird als das Gegenteil (oder die Umkehrung) des Vektors c bezeichnet.
In der Physik ist jeder Vektor mit einem bestimmten Inhalt gefüllt, und beim Vergleich gleichartiger Vektoren (z. B. Kräfte) können auch die Anwendungspunkte von Bedeutung sein.
2. Bestimmung der Projektion, Achse und Koordinate des Punktes.
Achse- Dies ist eine gerade Linie, der eine Richtung gegeben ist.
Eine Achse wird durch einen Buchstaben bezeichnet: X, Y, Z, s, t... Normalerweise wird (willkürlich) ein Punkt auf der Achse ausgewählt, der Ursprung genannt wird und in der Regel mit dem Buchstaben O bezeichnet wird. Von diesem Punkt aus werden die Entfernungen zu anderen für uns interessanten Punkten gemessen.
Projektion eines Punktes auf einer Achse ist die Basis einer Senkrechten, die von diesem Punkt auf eine gegebene Achse gezogen wird. Das heißt, die Projektion eines Punktes auf die Achse ist ein Punkt.
Punktkoordinate auf einer bestimmten Achse ist eine Zahl, deren Absolutwert der Länge des Achsensegments (im ausgewählten Maßstab) entspricht, das zwischen dem Ursprung der Achse und der Projektion des Punktes auf diese Achse liegt. Diese Zahl wird mit einem Pluszeichen angegeben, wenn die Projektion des Punktes in Richtung der Achse von ihrem Ursprung aus liegt, und mit einem Minuszeichen, wenn sie in der entgegengesetzten Richtung liegt.
3. Projektion des Vektors auf die Achse.
Die Projektion eines Vektors auf eine Achse ist ein Vektor, der durch Multiplikation der skalaren Projektion eines Vektors auf diese Achse und des Einheitsvektors dieser Achse erhalten wird. Wenn beispielsweise a x die Skalarprojektion des Vektors a auf die X-Achse ist, dann ist a x ·i seine Vektorprojektion auf diese Achse.
Bezeichnen wir die Vektorprojektion auf die gleiche Weise wie den Vektor selbst, jedoch mit dem Index der Achse, auf die der Vektor projiziert wird. Daher bezeichnen wir die Vektorprojektion des Vektors a auf die X-Achse als a x (ein fetter Buchstabe, der den Vektor bezeichnet, und der Index des Achsennamens) oder
(ein Buchstabe in niedriger Fettschrift, der einen Vektor bezeichnet, aber mit einem Pfeil oben (!) und einem tiefgestellten Index für den Achsennamen).Skalare Projektion Vektor pro Achse heißt Nummer, dessen absoluter Wert gleich der Länge des Achsensegments (im ausgewählten Maßstab) ist, das zwischen den Projektionen des Startpunkts und des Endpunkts des Vektors eingeschlossen ist. Normalerweise anstelle des Ausdrucks Skalarprojektion sie sagen einfach - Projektion. Die Projektion wird mit demselben Buchstaben wie der projizierte Vektor (in normaler, nicht fetter Schrift) bezeichnet, mit einem niedrigeren Index (in der Regel) des Namens der Achse, auf die dieser Vektor projiziert wird. Wenn beispielsweise ein Vektor auf die X-Achse projiziert wird A, dann wird seine Projektion mit a x bezeichnet. Wenn derselbe Vektor auf eine andere Achse projiziert wird und die Achse Y ist, wird ihre Projektion als y bezeichnet.
Um die Projektion zu berechnen Vektor Auf einer Achse (zum Beispiel der X-Achse) ist es notwendig, die Koordinate des Startpunkts von der Koordinate ihres Endpunkts zu subtrahieren
a x = x k − x n.
Die Projektion eines Vektors auf eine Achse ist eine Zahl. Darüber hinaus kann die Projektion positiv sein, wenn der Wert x k größer als der Wert x n ist,
negativ, wenn der Wert x k kleiner als der Wert x n ist
und gleich Null, wenn x k gleich x n ist.
Die Projektion eines Vektors auf eine Achse kann auch ermittelt werden, indem man den Modul des Vektors und den Winkel kennt, den er mit dieser Achse bildet.
Aus der Abbildung wird deutlich, dass a x = a Cos α
Das heißt, die Projektion des Vektors auf die Achse ist gleich dem Produkt aus dem Modul des Vektors und dem Kosinus des Winkels zwischen der Richtung der Achse und Vektorrichtung. Wenn der Winkel spitz ist, dann
Cos α > 0 und a x > 0, und wenn stumpf, dann ist der Kosinus des stumpfen Winkels negativ, und die Projektion des Vektors auf die Achse ist ebenfalls negativ.
Winkel, die von der Achse gegen den Uhrzeigersinn gemessen werden, gelten als positiv, und Winkel, die entlang der Achse gemessen werden, sind negativ. Da der Kosinus jedoch eine gerade Funktion ist, also Cos α = Cos (− α), können Winkel bei der Berechnung von Projektionen sowohl im Uhrzeigersinn als auch gegen den Uhrzeigersinn gezählt werden.
Um die Projektion eines Vektors auf eine Achse zu ermitteln, muss der Modul dieses Vektors mit dem Kosinus des Winkels zwischen der Richtung der Achse und der Richtung des Vektors multipliziert werden.
4. Grundformel der Vektoralgebra.
Projizieren wir den Vektor a auf die X- und Y-Achse des rechteckigen Koordinatensystems. Suchen wir die Vektorprojektionen des Vektors a auf diesen Achsen:
a x = a x ·i und y = a y ·j.
Aber gemäß der Regel der Vektoraddition
a = a x + a y.
a = a x i + a y j.
Wir haben also einen Vektor durch seine Projektionen und Vektoren des rechtwinkligen Koordinatensystems (oder durch seine Vektorprojektionen) ausgedrückt.
Vektorprojektionen a x und a y werden Komponenten oder Komponenten des Vektors a genannt. Die von uns durchgeführte Operation wird als Zerlegung eines Vektors entlang der Achsen eines rechteckigen Koordinatensystems bezeichnet.
Wenn der Vektor im Raum gegeben ist, dann
a = a x i + a y j + a z k.
Diese Formel wird als Grundformel der Vektoralgebra bezeichnet. Natürlich kann man es so schreiben.
Die l-Achse sei im Raum gegeben, also eine gerichtete Gerade.
Die Projektion des Punktes M auf die l-Achse ist die Basis M 1 der Senkrechten MM 1, die vom Punkt zur Achse abgesenkt wird.
Punkt M 1 ist der Schnittpunkt der l-Achse mit einer Ebene, die senkrecht zur Achse durch Punkt M verläuft (siehe Abb. 7).
Liegt der Punkt M auf der l-Achse, dann stimmt die Projektion des Punktes M auf die Achse mit M1 überein.
Sei AB ein beliebiger Vektor (AB¹ 0). Bezeichnen wir mit A 1 und b 1 die Projektionen des Anfangs A bzw. des Endes B des Vektors AB auf die l-Achse und betrachten wir den Vektor A 1 B 1
Die Projektion des Vektors AB auf die l-Achse ist die positive Zahl |A 1 B 1 | , wenn der Vektor A 1 B 1 und die l-Achse gleich gerichtet sind und die negative Zahl |A 1 B 1 | ist , wenn der Vektor A 1 B 1 und die l-Achse entgegengesetzt gerichtet sind (siehe Abb. 8). Wenn die Punkte a 1 und b 1 zusammenfallen (A 1 B 1 = 0), dann ist die Projektion des Vektors AB gleich 0.
Die Projektion des Vektors AB auf die l-Achse wird wie folgt bezeichnet: pr l AB. Wenn AB=0 oder AB^l, dann ist pr l AB=0.
Der Winkel j zwischen dem Vektor a und der l-Achse (oder der Winkel zwischen zwei Vektoren) ist in Abbildung 9 dargestellt. Offensichtlich 0£j£p
Schauen wir uns einige grundlegende Eigenschaften von Projektionen an.
Eigenschaft 1. Die Projektion des Vektors a auf die l-Achse ist gleich dem Produkt aus dem Modul des Vektors a und dem Kosinus des Winkels j zwischen dem Vektor und der Achse, d. h. pr l a =|a | cos j .
Folgerung 5.1. Die Projektion des Vektors auf die Achse ist positiv (negativ), wenn der Vektor mit der Achse einen spitzen (stumpfen) Winkel bildet, und ist gleich Null, wenn dieser Winkel recht ist.
Folgerung 5.2. Projektionen gleicher Vektoren auf dieselbe Achse sind einander gleich.
Eigenschaft 2. Die Projektion der Summe mehrerer Vektoren auf dieselbe Achse ist gleich der Summe ihrer Projektionen auf diese Achse
Eigenschaft 3. Wenn ein Vektor a mit einer Zahl A multipliziert wird, wird auch seine Projektion auf die Achse mit dieser Zahl multipliziert, d.h.
Somit führen lineare Operationen an Vektoren zu entsprechenden linearen Operationen an den Projektionen dieser Vektoren.
5.4. Zerlegung eines Vektors in Einheitsvektoren von Koordinatenachsen.
Vektormodul. Richtungskosinus.
Betrachten wir ein rechteckiges Koordinatensystem Oxyz im Raum. Wählen wir Einheitsvektoren (Orts) auf den Koordinatenachsen Ox, Oy und Oz aus, bezeichnet mit i, j, k (siehe Abb. 12).
Wählen wir einen beliebigen Raumvektor a und ordnen seinen Ursprung dem Koordinatenursprung zu: a = OM.
Finden wir die Projektionen des Vektors a auf die Koordinatenachsen. Zeichnen wir durch das Ende des Vektors OM Ebenen parallel zu den Koordinatenebenen. Die Schnittpunkte dieser Ebenen mit den Achsen bezeichnen wir mit M 1, M 2 bzw. M3. Wir erhalten ein rechteckiges Parallelepiped, dessen Diagonale der Vektor OM ist. Dann ist pr x a=|OM 1 |, np y a = |OM 2 |, pr z a=|OM3|. Indem wir die Summe mehrerer Vektoren definieren, finden wir a = OM 1 + M 1 N + NM.
Und da M 1 N=OM 2, NM = OM3, dann
a=OM 1 + OM 2 + OM 3 (5.1)
Bezeichnen wir die Projektionen des Vektors a=OM auf die Ox-, Oy- und Oz-Achsen jeweils mit a x, a y und a z, d. h. |OM 1 | = a x,|OM 2 | = a y, |OM 3 | = ein z . Dann erhalten wir aus den Gleichungen (5.1) und (5.2).
a=a x i+a y j+a z k (5.3)
Diese Formel ist grundlegend in der Vektorrechnung und wird als Zerlegung eines Vektors in Einheitsvektoren von Koordinatenachsen bezeichnet. Die Zahlen a x, a y, a z heißen die Koordinaten des Vektors a, d.h. die Koordinaten des Vektors sind seine Projektionen auf die entsprechenden Koordinatenachsen.
Die Vektorgleichheit (5.3) wird oft in symbolischer Form geschrieben: a = (a x ;a y ;a z).
Die Gleichheit b = (b x; b y; b z) bedeutet, dass b = b x i + b y j + b z k. Wenn Sie die Projektionen des Vektors a kennen, können Sie leicht einen Ausdruck für den Modul des Vektors finden. Basierend auf dem Satz über die Länge der Diagonale eines rechteckigen Parallelepipeds können wir schreiben
Das heißt, der Modul eines Vektors ist gleich der Quadratwurzel der Summe der Quadrate seiner Projektionen auf die Koordinatenachsen.
Die Winkel des Vektors a mit den Achsen Ox, Oy und Oz seien jeweils gleich a, b, g. Aufgrund der Eigenschaft der Vektorprojektion auf die Achse gilt
Oder was ist das Gleiche?
Die Zahlen heißen Richtungskosinus des Vektors a.
Wenn wir die Ausdrücke (5.5) in die Gleichung (5.4) einsetzen, erhalten wir
Durch Reduzieren erhalten wir die Relation
Das heißt, die Summe der Quadrate der Richtungskosinuswerte eines Vektors ungleich Null ist gleich eins.
Es ist leicht zu erkennen, dass die Koordinaten des Einheitsvektors e die Zahlen sind
Durch Angabe der Koordinaten eines Vektors können Sie also jederzeit dessen Größe und Richtung bestimmen, d.h. der Vektor selbst.
Algebraische Projektion eines Vektors auf jeder Achse ist gleich dem Produkt aus der Länge des Vektors und dem Kosinus des Winkels zwischen der Achse und dem Vektor:Pr a b = |b|cos(a,b) oder
Dabei ist a b das Skalarprodukt von Vektoren, |a| - Modul des Vektors a.
Anweisungen. Um die Projektion des Vektors Pr a b online zu finden, müssen Sie die Koordinaten der Vektoren a und b angeben. In diesem Fall kann der Vektor in der Ebene (zwei Koordinaten) und im Raum (drei Koordinaten) angegeben werden. Die resultierende Lösung wird in einer Word-Datei gespeichert. Wenn Vektoren durch die Koordinaten von Punkten angegeben werden, müssen Sie diesen Rechner verwenden.
Klassifizierung von Vektorprojektionen
Arten von Projektionen per Definition Vektorprojektion
- Die geometrische Projektion des Vektors AB auf die Achse (Vektor) wird als Vektor A"B" bezeichnet, dessen Anfang A' die Projektion des Anfangs A auf die Achse (Vektor) und dessen Ende B' die Projektion ist des Endes B auf die gleiche Achse.
- Die algebraische Projektion des Vektors AB auf die Achse (Vektor) wird als Länge des Vektors A"B" bezeichnet und mit einem + oder - Vorzeichen angegeben, je nachdem, ob der Vektor A"B" dieselbe Richtung wie die Achse hat ( Vektor).
Arten von Projektionen nach dem Koordinatensystem
Vektorprojektionseigenschaften
- Die geometrische Projektion eines Vektors ist ein Vektor (hat eine Richtung).
- Die algebraische Projektion eines Vektors ist eine Zahl.
Vektorprojektionssätze
Satz 1. Die Projektion der Summe der Vektoren auf eine beliebige Achse ist gleich der Projektion der Summanden der Vektoren auf dieselbe Achse.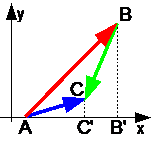 AC" =AB" +B"C"
AC" =AB" +B"C"
Satz 2. Die algebraische Projektion eines Vektors auf eine beliebige Achse ist gleich dem Produkt aus der Länge des Vektors und dem Kosinus des Winkels zwischen der Achse und dem Vektor:
Pr a b = |b|·cos(a,b)
Arten von Vektorprojektionen
- Projektion auf die OX-Achse.
- Projektion auf die OY-Achse.
- Projektion auf einen Vektor.
| Projektion auf der OX-Achse | Projektion auf der OY-Achse | Projektion auf Vektor |
Wenn die Richtung des Vektors A’B’ mit der Richtung der OX-Achse übereinstimmt, dann hat die Projektion des Vektors A’B’ ein positives Vorzeichen.  | Wenn die Richtung des Vektors A’B’ mit der Richtung der OY-Achse übereinstimmt, dann hat die Projektion des Vektors A’B’ ein positives Vorzeichen.  | Wenn die Richtung des Vektors A’B’ mit der Richtung des Vektors NM übereinstimmt, dann hat die Projektion des Vektors A’B’ ein positives Vorzeichen.  |
Wenn die Richtung des Vektors der Richtung der OX-Achse entgegengesetzt ist, dann hat die Projektion des Vektors A’B’ negatives Zeichen.
 | Wenn die Richtung des Vektors A’B’ der Richtung der OY-Achse entgegengesetzt ist, dann hat die Projektion des Vektors A’B’ ein negatives Vorzeichen. | Wenn die Richtung des Vektors A’B’ der Richtung des Vektors NM entgegengesetzt ist, dann hat die Projektion des Vektors A’B’ ein negatives Vorzeichen.  |
Wenn der Vektor AB parallel zur OX-Achse ist, ist die Projektion des Vektors A’B’ gleich dem Absolutwert des Vektors AB.   | Wenn der Vektor AB parallel zur OY-Achse ist, ist die Projektion des Vektors A’B’ gleich dem Absolutwert des Vektors AB.   | Wenn der Vektor AB parallel zum Vektor NM ist, ist die Projektion des Vektors A’B’ gleich dem Absolutwert des Vektors AB.   |
Wenn der Vektor AB senkrecht zur Achse OX steht, ist die Projektion A’B’ gleich Null (Nullvektor).   | Wenn der Vektor AB senkrecht zur OY-Achse steht, ist die Projektion A’B’ gleich Null (Nullvektor).   | Wenn der Vektor AB senkrecht zum Vektor NM steht, ist die Projektion A’B’ gleich Null (Nullvektor).   |
1. Frage: Kann die Projektion eines Vektors ein negatives Vorzeichen haben? Antwort: Ja, der Projektionsvektor kann ein negativer Wert sein. In diesem Fall hat der Vektor die entgegengesetzte Richtung (siehe, wie die OX-Achse und der AB-Vektor gerichtet sind)
2. Frage: Kann die Projektion eines Vektors mit dem Absolutwert des Vektors übereinstimmen? Antwort: Ja, das kann es. In diesem Fall sind die Vektoren parallel (oder liegen auf derselben Geraden).
3. Frage: Kann die Projektion eines Vektors gleich Null sein (Nullvektor)? Antwort: Ja, das kann es. In diesem Fall steht der Vektor senkrecht zur entsprechenden Achse (Vektor).
Beispiel 1. Der Vektor (Abb. 1) bildet mit der OX-Achse einen Winkel von 60° (er wird durch Vektor a angegeben). Wenn OE eine Skaleneinheit ist, dann ist |b|=4, also ![]() .
.

Tatsächlich ist die Länge des Vektors (geometrische Projektion b) gleich 2 und die Richtung stimmt mit der Richtung der OX-Achse überein.
Beispiel 2. Der Vektor (Abb. 2) bildet mit der OX-Achse (mit Vektor a) einen Winkel (a,b) = 120 °. Länge |b| Vektor b ist gleich 4, also pr a b=4·cos120 o = -2. 
Tatsächlich beträgt die Länge des Vektors 2 und die Richtung ist entgegengesetzt zur Richtung der Achse.