Diskretinio atsitiktinio dydžio pasiskirstymo dėsnis. Problemų sprendimo pavyzdžiai. Normalusis atsitiktinių dydžių pasiskirstymo dėsnis Trys atsitiktinių dydžių pasiskirstymo dėsniai

Kintamasis vadinamas atsitiktinis, jei dėl patirties jis su tam tikromis tikimybėmis gali įgyti tikrąsias vertybes. Išsamiausia, visapusiškiausia atsitiktinio dydžio charakteristika yra pasiskirstymo dėsnis. Paskirstymo dėsnis– funkcija (lentelė, grafikas, formulė), leidžianti nustatyti tikimybę, kad atsitiktinis dydis Xįgauna tam tikrą vertę Xi arba patenka į tam tikrą intervalą. Jei atsitiktinis dydis turi duotą pasiskirstymo dėsnį, tada sakoma, kad jis paskirstomas pagal šį dėsnį arba paklūsta šiam pasiskirstymo dėsniui.

Atsitiktinė vertė X paskambino diskretus, jei toks yra neneigiama funkcija

kuri atitinka vertę Xi kintamasis X tikimybė Ri, su kuriuo ji įgyja šią vertę.

Atsitiktinė vertė X paskambino tęstinis, jei kam a < b yra tokia neneigiama funkcija f (x), Ką

(2)

Funkcija f (x) vadinamas pasiskirstymo tankis nuolatinis atsitiktinis dydis.

Tikimybė, kad atsitiktinis kintamasis X(diskretus arba tęstinis) įgauna reikšmę, mažesnę nei X, paskambino paskirstymo funkcija atsitiktinis kintamasis X ir yra paskirtas F (x) :

(3)

Pasiskirstymo funkcija yra universalus pasiskirstymo dėsnio tipas, tinkantis bet kuriam atsitiktiniam dydžiui.

Bendrosios paskirstymo funkcijos savybės:

(4)

Be šio universalaus, yra ir tam tikrų rūšių paskirstymo dėsnių: platinimo serija(tik diskretiesiems atsitiktiniams dydžiams) ir pasiskirstymo tankis(tik nuolatiniams atsitiktiniams dydžiams).

Pagrindinės pasiskirstymo tankio savybės:

(5)

Kiekvienas pasiskirstymo dėsnis yra funkcija, visiškai apibūdinanti atsitiktinį kintamąjį tikimybiniu požiūriu. Praktiškai apie atsitiktinio dydžio tikimybių skirstinį X Dažnai turime spręsti tik pagal testų rezultatus. Kartodami testus, kiekvieną kartą fiksuosime, ar įvyko atsitiktinis mus dominantis įvykis A, arba ne. Santykinis dažnis(arba tiesiog dažnis) atsitiktinis įvykis A vadinamas skaičių santykiu nA viso šio įvykio atvejų n atlikti bandymai. Tuo pačiu metu pripažįstame, kad atsitiktinių įvykių santykinis dažnis yra artimas jų tikimybei. Tai juo labiau tiesa, kuo daugiau atliekamų eksperimentų. Šiuo atveju dažniai, kaip ir tikimybės, turėtų būti priskirti ne atskiroms atsitiktinio dydžio reikšmėms, o intervalams. Tai reiškia, kad visas galimų atsitiktinio dydžio verčių diapazonas X reikia suskirstyti į intervalus. Atlikdami daugybę testų, kurie suteikia empirines vertes X, reikia pataisyti skaičius nx kiekvieno intervalo rezultatų hitai. Su daugybe testų n požiūris n x / n(patekimo į intervalus dažniai) turėtų būti artimi tikimybei patekti į šiuos intervalus. Priklausomybė nuo dažnio n x / n nustato iš intervalų empirinis pasiskirstymas atsitiktinių kintamųjų tikimybės X, kurio grafinis vaizdavimas vadinamas histograma(1 pav.).

Ryžiai. 1. Histograma ir niveliavimo pasiskirstymo tankis

Norėdami sudaryti histogramą, išilgai abscisių ašies nubraižomi vienodo ilgio intervalai, į kuriuos padalinamas visas galimų atsitiktinio dydžio verčių diapazonas. X, o dažniai brėžiami išilgai ordinačių ašies n x / n. Tada kiekvienos histogramos juostos aukštis yra lygus atitinkamam dažniui. Taigi gauname apytikslį atsitiktinio dydžio tikimybių pasiskirstymo dėsnio vaizdą Xžingsninės funkcijos pavidalu, kurios aproksimacija (išlygiavimas) į kokią nors kreivę f(x) duos pasiskirstymo tankį.

Tačiau dažnai pakanka nurodyti tik atskirus skaitinius parametrus, apibūdinančius pagrindines skirstinio savybes. Šie skaičiai vadinami atsitiktinio dydžio skaitinėmis charakteristikomis.

Normalaus pasiskirstymo tankis turi tokią formą:

Kur a- tam tikro atsitiktinio dydžio tikimybių skirstinio arba matematinio lūkesčio centras, t.y.

tam tikro atsitiktinio dydžio standartinis nuokrypis.

Praktikoje apskaičiuojami atitinkami statistiniai įverčiai. Taigi matematinio lūkesčio įvertis bus vidutinė vertė:

kur yra duomenų kiekis nagrinėjamame statistiniame masyve.

Matematinis lūkestis yra teorinė tam tikro atsitiktinio dydžio, kurio vidutinė vertė neribotai didėja duomenų kiekiui, reikšmė.

Standartinis nuokrypis:

Logistikoje ta ar kita kiekio vertė įvertinama pagal vertę

šiuo atveju variacijos koeficientas apskaičiuojamas:

4 paveiksle parodytas normalaus tikimybių skirstinio grafikas.

4 pav. Normaliojo tikimybių pasiskirstymo dėsnis

Eksponentinio tikimybių skirstinio dėsnio tankis turi tokią formą:

kur yra natūraliojo logaritmo pagrindas.

Eksponentinis dėsnis apibūdina atsitiktinių logistinių procesų laiko parametrus. Šie atsitiktiniai dydžiai patenka į eksponentinį dėsnį:

1) klientų aptarnavimo laikas;

2) transporto priemonių pakrovimo ir iškrovimo laikas;

3) laikas, praleistas kitoms logistikos operacijoms

4) intervalas tarp prašymų gauti paslaugą.

Eksponentinio dėsnio ypatumas yra tas, kad jį lemia vienas parametras. Kuriame

kur yra tiriamo laiko parametro vidutinė reikšmė.

Dydžiams, kurie paklūsta eksponentiniam dėsniui, matematinė lūkestis M ir vidutinė kvadratinė reikšmė yra lygios viena kitai:

5 paveiksle parodytas eksponentinės dėsnio grafikas.

5 pav. Eksponentinio tikimybių pasiskirstymo dėsnis

Binarinio tikimybių skirstinio dėsnis

Tikimybių skirstinio dvinario dėsnis išreiškiamas formule:

Šis dėsnis nustato įvykių tikimybę iš bendro įvykių skaičiaus

kur yra vieno įvykio iš tam tikros įvykių grupės tikimybė;

tikimybė, kad nurodytas įvykis neįvyks,

Vertė yra derinių skaičius Autorius , nustatoma pagal formulę:

Norint apskaičiuoti derinių skaičių, naudojama lygybė:

Naudojant binominį skirstinį, labiausiai tikėtinas įvykių skaičius yra:

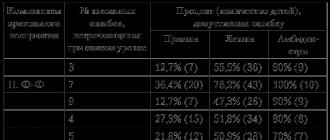
Tikimybių skirstymo dėsnių palyginimas. Susitarimo kriterijus

Tikimybių teorijoje yra metodų, kurie leidžia įvertinti faktinių tikimybių skirstinių atitikimo laipsnį jų teorinėms reikšmėms. Tam naudojami vadinamieji susitarimo kriterijai, iš kurių žinomiausias yra kriterijus. Šis kriterijus leidžia palyginti empirinius pasiskirstymo dėsnius, gautus iš tų pačių faktinių duomenų.

Kuo mažesnė reikšmė, tuo geriau šis empirinis dėsnis sutampa su teoriniu. Norint palyginti empirinius tikimybių pasiskirstymo dėsnius, vertės apskaičiuojamos pagal šią formulę:

Kur yra atitinkamai faktinės ir teorinės tiriamų paskirstymo dėsnių dažnių vertės.

Vertė taip pat yra atsitiktinė, todėl paklūsta savo paskirstymo dėsniui. Empirinio pasiskirstymo dėsnių palyginimo metodą galima iliustruoti pavyzdžiu.

Nustatykime, kuris tikimybių pasiskirstymo dėsnis – normalusis ar eksponentinis – geriau atspindi tam tikro dydžio pasiskirstymą, t.y. Patikrinkime hipotezes. Kaip tiriamą vertę laikome tam tikros prekės pardavimo apimtį. Pradiniai duomenys pateikti 3 lentelėje:

Lentelė 3. Informacija apie prekių pardavimą

Užduotis formuluojama taip: sudaryti tam tikros prekės paklausos dydžio tikimybių pasiskirstymą, jei atlikus tyrimą gaunami pardavimo rezultatai, tūkstančiais rublių. per dieną.

Problemos sprendimas pateiktas 4 priede.

Bendru atveju, nemažai logistikos procesų, būtent: pardavimas, produkcijos siuntimas iš didmeninės prekybos įmonių, atsargų judėjimas, produkcijos tiekimo paslaugų teikimas, materialinių išteklių sunaudojimas ir kt. aprašytas normaliojo tikimybių skirstinio dėsniu. Išskirtinis šio skirstinio bruožas yra ryški atsitiktinių dydžių simetrija, palyginti su jų vidutine verte. Šiems procesams įprastas įstatymas taikomas visiems gaminiams, tam tikroms prekių grupėms ar atskiroms prekių vienetams.

Atliekant logistikos procesų struktūros ABC analizę, gautos charakteristikos verte arba fizine išraiška priklauso nuo eksponentinio pasiskirstymo.

Tai, kad gaminių pardavimas atitinka įprastą dėsnį, yra svarbus logistikai, nes tai leidžia mums nustatyti vertę inventorius, kuriai rekomenduojama naudoti šią formulę:

kur yra reikalingas atsargų kiekis neribotam laikui,

vidutiniai pardavimai per laiko vienetą (dieną, savaitę, mėnesį),

standartinis nuokrypis.

Nagrinėjamame pavyzdyje inventorius yra lygus:

Šis modelis rodo, kad bet kuris pirkėjo reikalavimas tam tikrai produkto kokybei turi būti patenkintas tikimybe, artima 1. Šiame modelyje naudojama „trijų sigmų“ taisyklė. Pagal įprastą dėsnį tai atitinka 0,99 tikimybę.

IN šiuolaikinėmis sąlygomis Kompiuterinės technologijos leidžia sekti vidutinius pardavimus ir standartinius nuokrypius esamu laiko režimu bei koreguoti atsargų kiekį.

Pateiktas atsargų nustatymo modelis gali būti naudojamas tiek mažmeninei, tiek didmeninei prekybai.

PASKIRSTYMO DĖSNIS IR CHARAKTERISTIKOS

ATSITIKTINIAI KINTAMAI

Atsitiktiniai kintamieji, jų klasifikacija ir aprašymo metodai.

Atsitiktinis dydis – tai dydis, kuris eksperimento rezultatu gali įgyti vienokią ar kitokią reikšmę, bet kuris iš anksto nėra žinomas. Todėl atsitiktiniam dydžiui galite nurodyti tik reikšmes, kurių vienos tikrai reikės kaip eksperimento rezultatą. Toliau šias reikšmes vadinsime galimomis atsitiktinio dydžio reikšmėmis. Kadangi atsitiktinis dydis kiekybiškai apibūdina atsitiktinį eksperimento rezultatą, jį galima laikyti kiekybine atsitiktinio įvykio charakteristika.

Atsitiktiniai kintamieji paprastai žymimi lotyniškos abėcėlės didžiosiomis raidėmis, pavyzdžiui, X..Y..Z, o galimos jų reikšmės – atitinkamomis mažomis raidėmis.

Yra trijų tipų atsitiktiniai dydžiai:

Diskretus; Nepertraukiamas; Mišrus.

Diskretus yra atsitiktinis dydis, kurio galimų reikšmių skaičius sudaro skaičiuojamą aibę. Savo ruožtu aibė, kurios elementus galima sunumeruoti, vadinama skaičiuojama. Žodis „diskretus“ kilęs iš lotyniško žodžio discretus, reiškiančio „nepertraukiamas, susidedantis iš atskirų dalių“.

1 pavyzdys. Diskretusis atsitiktinis dydis yra sugedusių dalių X skaičius nproduktų partijoje. Iš tiesų, galimos šio atsitiktinio dydžio reikšmės yra sveikųjų skaičių nuo 0 iki n.

2 pavyzdys. Diskretusis atsitiktinis kintamasis yra šūvių skaičius prieš pirmąjį pataikymą į taikinį. Čia, kaip ir 1 pavyzdyje, galimos reikšmės gali būti sunumeruotos, nors ribiniu atveju galima reikšmė yra be galo didelis skaičius.

Nuolatinis yra atsitiktinis dydis, kurio galimos reikšmės nuolat užpildo tam tikrą skaitinės ašies intervalą, kartais vadinamą šio atsitiktinio dydžio egzistavimo intervalu. Taigi bet kuriame baigtiniame egzistavimo intervale nuolatinio atsitiktinio dydžio galimų reikšmių skaičius yra be galo didelis.

3 pavyzdys. Nuolatinis atsitiktinis dydis yra įmonės elektros energijos suvartojimas per mėnesį.

4 pavyzdys. Nuolatinis atsitiktinis dydis yra paklaida matuojant aukštį naudojant aukščiamatį. Iš aukščiamačio veikimo principo aišku, kad paklaida yra intervale nuo 0 iki 2 m. Todėl šio atsitiktinio dydžio egzistavimo intervalas yra intervalas nuo 0 iki 2 m.

Atsitiktinių dydžių pasiskirstymo dėsnis.

Atsitiktinis dydis laikomas visiškai apibrėžtu, jei jo galimos reikšmės yra nurodytos skaitinėje ašyje ir nustatytas pasiskirstymo dėsnis.

Atsitiktinio dydžio pasiskirstymo dėsnis yra ryšys, nustatantis ryšį tarp galimų atsitiktinio dydžio verčių ir atitinkamų tikimybių.

Sakoma, kad atsitiktinis kintamasis yra paskirstytas pagal tam tikrą dėsnį arba jam taikomas tam tikras pasiskirstymo įstatymas. Kai kurie tikimybių, pasiskirstymo funkcijos, tikimybių tankio ir charakteristikų funkcijos yra naudojami kaip pasiskirstymo dėsniai.

Pasiskirstymo dėsnis pateikia išsamų tikėtiną atsitiktinio dydžio aprašymą. Pagal pasiskirstymo dėsnį, prieš eksperimentą galima nuspręsti, kurios galimos atsitiktinio dydžio reikšmės pasirodys dažniau, o kurios rečiau.

Diskrečiajam atsitiktiniam dydžiui pasiskirstymo dėsnį galima nurodyti lentelės pavidalu, analitiškai (formulės pavidalu) ir grafiškai.

Paprasčiausias diskretinio atsitiktinio dydžio pasiskirstymo dėsnio nurodymo būdas yra lentelė (matrica), kurioje didėjimo tvarka surašytos visos galimos atsitiktinio dydžio reikšmės ir jas atitinkančios tikimybės, t.y.

Tokia lentelė vadinama diskrečiojo atsitiktinio dydžio skirstinio seka. 1

Įvykiai X 1, X 2,..., X n, susidedantys iš to, kad atlikus testą atsitiktinis dydis X atitinkamai įgis x 1, x 2,... x n reikšmes. nenuoseklūs ir vieninteliai galimi (kadangi lentelėje pateikiamos visos galimos atsitiktinio dydžio reikšmės), t.y. sudaryti pilną grupę. Todėl jų tikimybių suma lygi 1. Taigi bet kuriam diskrečiajam atsitiktiniam dydžiui

(Šis vienetas kažkaip paskirstomas tarp atsitiktinio dydžio reikšmių, taigi ir terminas „paskirstymas“).

Pasiskirstymo eilutes galima pavaizduoti grafiškai, jei atsitiktinio dydžio reikšmės brėžiamos išilgai abscisių ašies, o jų atitinkamos tikimybės – išilgai ordinačių ašies. Sujungus gautus taškus, susidaro trūkinė linija, vadinama tikimybių skirstinio daugiakampiu arba daugiakampiu (1 pav.).

PavyzdysĮ loteriją įeina: automobilis, kurio vertė 5000 den. vnt., 4 televizoriai, kainuojantys 250 den. vnt., 5 vaizdo registratoriai, kurių vertė 200 den. vienetų Iš viso 7 dienoms parduodama 1000 bilietų. vienetų Sudarykite loterijos dalyvio, įsigijusio vieną bilietą, grynųjų laimėjimų paskirstymo įstatymą.

Sprendimas. Galimos atsitiktinio dydžio X reikšmės - grynasis laimėjimas už bilietą - yra lygios 0-7 = -7 pinigai. vienetų (jei bilietas nelaimėjo), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 den. vienetų (jei biliete yra atitinkamai vaizdo grotuvo, televizoriaus ar automobilio laimėjimai). Atsižvelgdami į tai, kad iš 1000 bilietų nelaimėjusiųjų skaičius yra 990, o nurodyti laimėjimai yra atitinkamai 5, 4 ir 1, ir naudojant klasikinį tikimybės apibrėžimą, gauname.

Atsitiktinis yra dydis, kuris dėl testavimo gali įgyti vienokią ar kitokią galimą reikšmę, kuri iš anksto nežinoma. Yra diskretieji ir nuolatiniai atsitiktiniai dydžiai.
Jei atsitiktinio dydžio galimų reikšmių aibė yra baigtinė arba sudaro begalinę skaičių seka, tada toks atsitiktinis dydis vadinamas diskretus (3.1, 3.3, 3.4 pavyzdžiai).
Vadinamas atsitiktinis dydis, kurio reikšmių rinkinys visiškai užpildo tam tikrą skaitinį intervalą tęstinis (3.2 pavyzdys). Atminkite, kad diskretieji ir nuolatiniai kintamieji neišnaudoja visų tipų atsitiktinių kintamųjų.
Jei atsitiktinis dydis nepriklauso nei diskretiesiems, nei tęstiniams atsitiktiniams dydžiams, tada jis vadinamas sumaišytas .
Akivaizdu, kad už visas charakteristikas Diskrečiajam atsitiktiniam dydžiui nepakanka žinoti jo reikšmę. Jie turi būti suderinti su tikimybėmis.
Vadinamas visų galimų diskretinio atsitiktinio dydžio reikšmių ir jų tikimybių atitikimas paskirstymo dėsnis duotas atsitiktinis dydis.
Paprasčiausias diskretinio atsitiktinio dydžio pasiskirstymo dėsnio nurodymo būdas yra lentelė, kurioje pateikiamos galimos atsitiktinio dydžio reikšmės (dažniausiai didėjančia tvarka) ir atitinkamos tikimybės:

Tokia lentelė vadinama paskirstymo serija. Tarkime, kad atsitiktinio dydžio galimų reikšmių skaičius yra baigtinis: X 1 , X 2 , …, x n. Vieno bandymo metu atsitiktinis kintamasis įgauna vieną ir tik vieną pastovią reikšmę. Todėl įvykiai X = x i (i = 1, 2, … , n) sudaro visą porų nepriklausomų įvykių grupę. Vadinasi, R 1 + R 2 + … + р n = 1.
Pasiskirstymo dėsnį taip pat galima pavaizduoti grafiškai, abscisių ašyje nubraižant galimas atsitiktinio dydžio reikšmes, o ordinačių ašyje – atitinkamas tikimybes. Siekiant didesnio išraiškingumo, gauti taškai sujungiami tiesiais segmentais. Gauta figūra vadinama paskirstymo daugiakampiu (daugiakampiu).
Yra keli platinimo dėsniai:

Dvejetainė

nuodai

· Normalus (Gausso)

· Eksponentinis

Uniforma

Binominis skirstinys atsitiktinis kintamasis

n – testų skaičius

Puasono pasiskirstymas.
Situacija, kai kiekvieno bandymo įvykio tikimybė yra artima 0 (tokie įvykiai vadinami retais įvykiais), o bandymų skaičius yra didelis. Tikimybė, kad įvykis įvyks m kartų per n nepriklausomų bandymų, yra maždaug lygi:

n – testų skaičius
m – numatomas norimo įvykio įvykis
p – įvykio įvykimo viename bandyme tikimybė
Pavyzdys: Nustatyta, kad vežime vežant daugiau nei 5000 gaminių, vidutiniškai sugenda viena prekė. Raskite tikimybę, kad trys produktai suges. (0,06).

– Matematinis lūkestis

Sklaida

Eksponentinis pasiskirstymas

- intensyvumas (vidutinis įvykių skaičius per laiko vienetą)

Ištisinis atsitiktinis dydis X, kurio tankio funkcija pateikiama šia išraiška, vadinamas atsitiktiniu dydžiu, turinčiu eksponentinį, arba eksponentinį, pasiskirstymą.

Tarnavimo trukmė įvairių įrenginių o atskirų šių įrenginių elementų be gedimų veikimo laikas, kai tenkinamos tam tikros sąlygos, dažniausiai paklūsta eksponentiniam pasiskirstymui. Kitaip tariant, laikas tarp dviejų vienas po kito einančių retų įvykių dažnai pasiskirsto pagal eksponentinį pasiskirstymą.

Kaip matyti iš formulės, eksponentinį skirstinį lemia tik vienas parametras. Ši eksponentinio skirstinio savybė rodo jos pranašumą, palyginti su skirstiniais, kurie priklauso nuo didesnio parametrų skaičiaus.

Eksponentinio pasiskirstymo funkcijų grafikas atrodo taip:

Tikimybė, kad atsitiktinis dydis X pateks į intervalą:

,tikėtina vertė

, dispersija

Standartinis nuokrypis

Taigi eksponentiniam skirstiniui būdinga tai, kad standartinis nuokrypis yra skaitiniu požiūriu lygus matematiniam lūkesčiui.

Vienodas paskirstymas
Vienodas tikimybių skirstinys yra paprasčiausias ir gali būti diskretinis arba tęstinis. Diskretus vienodas pasiskirstymas yra pasiskirstymas, kurio kiekvienos SV reikšmės tikimybė yra tokia pati, tai yra:

kur N yra galimų SV reikšmių skaičius.

Ištisinio CB X tikimybių pasiskirstymas, paimant visas jo reikšmes iš atkarpos [a;b], vadinamas vienodu, jei jo tikimybių tankis šiame atkarpoje yra pastovus, o už jo ribų lygus nuliui:

11.Skirstymo funkcija ir jos savybės.

Paskirstymo funkcija atsitiktinis kintamasis X yra tikimybė, kad jos reikšmė bus mažesnė už funkcijos argumentą x:

F(x)=P( X<x}.

Geometriškai pasiskirstymo funkcija aiškinama kaip tikimybė, kad atsitiktinis taškas X nukris į kairę nuo duoto taško X. Iš geometrinės interpretacijos tai galima aiškiai nustatyti pagrindinės skirstymo funkcijos savybės.

1. F(-¥) = 0.

2. F(+¥) = 1.

3. F(x) yra nemažėjanti jo argumento funkcija, t.y. adresu x 1 < x 2

F(x 1) £ F(x 2).

4. P(α£ X < β) = F(β) - F(α), „[α,β[ОR. (5.4)

Tikimybė, kad atsitiktinis dydis X dėl eksperimento pateks į atkarpą nuo α iki β (įskaitant α) lygi paskirstymo funkcijos prieaugiui Aš esu šioje srityje.

Taigi bet kurio atsitiktinio dydžio pasiskirstymo funkcija F(x) yra nemažėjanti jo argumento funkcija, kurios reikšmės yra tarp 0 ir 1: 0≤F(x)≤1 ir F(-∞) =0, F(+∞)= 1.

12. Diskretinio ir nuolatinio atsitiktinio dydžio skirstinio funkcija.

Diskretinio atsitiktinio dydžio pasiskirstymo funkcija

Jei x yra diskretusis atsitiktinis kintamasis, imant reikšmes x 1 <x 2 < … <x i < … с вероятностями p 1 <p 2 < … <p i < …, то таблица вида

paskambino diskretinio atsitiktinio dydžio pasiskirstymas.

Atsitiktinio dydžio paskirstymo funkcija su tokiu skirstiniu turi formą

Diskretus atsitiktinis dydis turi žingsninio pasiskirstymo funkciją.

Nepertraukiamo atsitiktinio dydžio reikšmių rinkinys yra neskaičiuojamas ir paprastai reiškia tam tikrą baigtinį arba begalinį intervalą.

Iškviečiamas atsitiktinis dydis x(w), apibrėžtas tikimybių erdvėje (W, S, P). tęstinis(absoliučiai tęstinis) W, jei yra neneigiama funkcija, kad bet kokiam x pasiskirstymo funkcija Fx(x) gali būti pavaizduota kaip integralas

13. Ištisinio atsitiktinio dydžio pasiskirstymo tankis.

Funkcija vadinama funkcija tikimybių pasiskirstymo tankiai.

Apibrėžimas reiškia pasiskirstymo tankio funkcijos savybes:

1. Pasiskirstymo tankis yra neneigiamas: .

2. Tikimybių pasiskirstymo tankio visos skaičių tiesės integralas lygus vienetui:

3. Tolydumo taškuose pasiskirstymo tankis lygus skirstinio funkcijos išvestinei: .

4. Pasiskirstymo tankis lemia atsitiktinio dydžio pasiskirstymo dėsnį, nes jis nustato tikimybę, kad atsitiktinis dydis pateks į intervalą:

5. Tikimybė, kad nenutrūkstamas atsitiktinis dydis įgis tam tikrą reikšmę, lygi nuliui: . Todėl galioja šios lygybės:

Pasiskirstymo tankio funkcijos grafikas vadinamas pasiskirstymo kreivė, o plotas, ribojamas pasiskirstymo kreivės ir x ašies, yra lygus vienetui. Tada geometriškai pasiskirstymo funkcijos Fx(x) reikšmė taške x0 yra plotas, apribotas pasiskirstymo kreivės ir x ašies ir esantis į kairę nuo taško x0.

14. Pasiskirstymo funkcijos ir pasiskirstymo tankio ryšys. Integralinė visuminės tikimybės formulė.

Žinant pasiskirstymo tankį F(X), galime rasti paskirstymo funkciją F(X) pagal formulę

.

tikrai, F(X) = P(X< X ) = P(-∞< X < X) .

Vadinasi,

.

.

Taigi, Žinodami pasiskirstymo tankį, galite rasti pasiskirstymo funkciją. Žinoma, iš žinomos pasiskirstymo funkcijos galima rasti pasiskirstymo tankį, būtent:

F(X) = F"(X).
15. Atsitiktinių dydžių skaitinės charakteristikos.

Paskirstymo dėsnis visiškai apibūdina atsitiktinį kintamąjį su

tikimybinis požiūris. Tačiau dažnai pakanka nurodyti tik atskirą

Skaitiniai parametrai, leidžiantys išreikšti glausta forma

reikšmingiausius paskirstymo bruožus. Tokie parametrai vadinami

nustatomi atsitiktinio dydžio skaitinėmis charakteristikomis.

Tarp skaitinių charakteristikų galima išskirti charakteristikas

padėtis, t.y. tam tikros vidutinės, apytikslės atsitiktinio dydžio reikšmės

eilės, aplink kurias grupuojamos galimos jo vertės.

Skaitmeninės charakteristikos apima:

· Tikėtina vertė

· Dispersija

· Mediana

· Akimirkos

Kvantilė

Asimetrija

Ekscentriškumas

16.Matematinis atsitiktinio dydžio lūkestis ir jo savybės.

Tikėtina vertė - skaičius, aplink kurį sutelktos atsitiktinio dydžio reikšmės. Atsitiktinio dydžio x matematinis lūkestis žymimas M x.

Diskretaus atsitiktinio dydžio lūkestis x turintis paskirstymą

dydis vadinamas, jei atsitiktinio dydžio reikšmių skaičius yra baigtinis.

Jei atsitiktinio dydžio reikšmių skaičius yra skaičiuojamas, tada . Be to, jei dešinėje lygybės pusėje esanti eilutė skiriasi, sakoma, kad atsitiktinis kintamasis x neturi matematinių lūkesčių.

Ištisinio atsitiktinio dydžio tikėjimasis su tikimybės tankiu p x(x) apskaičiuojamas pagal formulę. Be to, jei integralas dešinėje lygybės pusėje skiriasi, tai atsitiktinis kintamasis x neturi matematinių lūkesčių.

Jei atsitiktinis dydis h yra atsitiktinio dydžio x funkcija, h = f(x), tai

.

Panašios formulės galioja ir diskrečiojo atsitiktinio dydžio funkcijoms:

, .

Pagrindinės matematinių lūkesčių savybės:

· matematinis konstantos lūkestis yra lygus šiai konstantai, M c=c ;

· matematinis lūkestis – tiesinis funkcinis atsitiktinių dydžių erdvėje, t.y. bet kuriems dviem atsitiktiniams dydžiams x, h ir savavališkoms konstantoms a Ir bšviesus: M (kirvis+ bh) = a M (x)+ b M (h);

matematinis dviejų sandaugos lūkestis nepriklausomas atsitiktiniai dydžiai yra lygūs jų matematinių lūkesčių sandaugai, t.y. M (x h) = M (x) M (h).

17. Atsitiktinio dydžio dispersija ir jo savybės.

Atsitiktinio dydžio dispersija apibūdina atsitiktinio dydžio sklaidą aplink jo matematinį lūkestį.

Jei atsitiktinis kintamasis x turi matematinį lūkestį M x, Tai dispersija atsitiktinis kintamasis x yra dydis D x =M (x - M x) 2 .

Tai lengva parodyti D x = M (x - M x) 2 =M x 2 - M (x)2.

Ši universali formulė vienodai tinka tiek diskretiesiems atsitiktiniams dydžiams, tiek nuolatiniams. Didumas M x 2 >atitinkamai diskretiesiems ir nuolatiniams atsitiktiniams dydžiams apskaičiuojamas pagal formules

, .

Jis dažnai naudojamas norint nustatyti atsitiktinio dydžio reikšmių sklaidos matą standartinis nuokrypis, susijęs su dispersija pagal ryšį .

Pagrindinės dispersijos savybės:

· bet kurio atsitiktinio dydžio dispersija yra neneigiama, D x 0;

· konstantos dispersija lygi nuliui, D c=0;

· savavališkai konstantai D (cx) = c 2 D (x);

· dviejų sumos dispersija nepriklausomas atsitiktiniai dydžiai, lygūs jų dispersijų sumai: D (x± h) = D (x) + D (h).

18. Atsitiktinio dydžio k eilės momentas, absoliutūs ir centriniai momentai.

Pradinis k-osios užsakymo momentas atsitiktinis dydis x vadinamas matematiniu lūkesčiu k atsitiktinio dydžio x laipsnis, t.y. a k = M x k.

Centrinis k-osios eilės momentas atsitiktinis kintamasis x yra reikšmė m k, apibrėžiamas formule m k = M (x - M x)k.

Atkreipkite dėmesį, kad atsitiktinio dydžio matematinis tikėjimasis yra pirmosios eilės pradinis momentas, 1 = M x, o sklaida yra pagrindinis momentas Antras užsakymas,

a 2 = M x 2 = M (x - M x) 2 =D x.

Yra formulių, leidžiančių per jį išreikšti centrinius atsitiktinio dydžio momentus pradines akimirkas, Pavyzdžiui:

m 2 =a 2 -a 1 2, m 3 = a 3 - 3a 2 ir 1 + 2a 1 3 .

Jei ištisinio atsitiktinio dydžio tikimybių pasiskirstymo tankis yra simetriškas tiesės atžvilgiu x = M x, tada visi jo centriniai nelyginės eilės momentai yra lygūs nuliui.

ABSOLIUTIS MOMENTAS

atsitiktinis dydis s X- matematinės lūkesčiai Įprastas A. m žymėjimas yra toks

Vadinamas skaičius r. eilės A. m. Jei F(x) yra pasiskirstymo funkcija X, Tai

ir, pavyzdžiui, jei skirstinio X tankis yra p(x) , Tai

19. Mada ir mada

atsitiktinis kintamasis X vadinamas labiausiai tikėtinu jo dydžiu, t.y.

kuriam tikimybė pi

arba pasiekiamas pasiskirstymo tankis f (x).

jie pasiekia maksimumą. Režimas paprastai žymimas Mx

Jei tikimybės daugiakampis arba pasiskirstymo tankis pasiekia maksimumą ties

keli taškai, tada tokie skirstiniai vadinami atsitiktinio dydžio multimodaline mediana.

Tolydinio atsitiktinio dydžio X mediana vadinama

kuriai duota jo reikšmė xm

20. Atsitiktinio dydžio skirstinio kvantinis lygmuo x.

-kvantilis atsitiktinis dydis su pasiskirstymo funkcija yra bet koks skaičius, atitinkantis dvi sąlygas:

2)

Atminkite, kad šios sąlygos yra lygiavertės šioms:

Jei – nuolat griežtai monotoniška funkcija, tada yra vienas bet kurios eilės kvantilis, kuris vienareikšmiškai nustatomas pagal lygtį ir todėl išreiškiamas per funkciją, atvirkštinę paskirstymo funkcijai:

Be nurodytos situacijos, kai lygtis turi unikalų sprendinį (kuris suteikia atitinkamą kvantilį), galimi ir kiti du:

§ jei nurodyta lygtis neturi sprendimų, tai reiškia, kad yra vienas taškas, kuriame paskirstymo funkcija turi nenutrūkstamumą, kuris tenkina šis apibrėžimas ir yra tvarkos kvantilis. Šiuo klausimu tenkinami šie santykiai: ir (pirmoji nelygybė yra griežta, o antroji gali būti arba griežta, arba virsti lygybe).

§ jei lygtis turi daugiau nei vienas sprendimas, tada visi jo sprendiniai sudaro intervalą, kuriame pasiskirstymo funkcija yra pastovi. Bet kuris šio intervalo taškas gali būti laikomas eilės kvantiliu. Reikšmingos išvados, kuriose dalyvauja kvantilis, reikšmingai nepasikeis, nes tikimybė, kad atsitiktinis dydis pateks į tam tikrą intervalą, yra lygi nuliui.

21. Atsitiktinio dydžio skirstinio asimetrija ir ekscentriškumas.

Asimetrija

Tikimybių teorijoje ir matematinėje statistikoje pasiskirstymo asimetrijos matas yra asimetrijos koeficientas, kuris nustatomas pagal formulę,

kur m 3 yra trečios eilės centrinis momentas, yra standartinis nuokrypis.

Normalus skirstinys dažniausiai naudojamas tikimybių teorijoje ir matematinėje statistikoje, todėl normaliojo skirstinio tikimybių tankio grafikas tapo savotišku etalonu, su kuriuo lyginami kiti skirstiniai. Vienas iš parametrų, nulemiančių skirtumą tarp atsitiktinio dydžio x ir normaliojo skirstinio, yra kurtozė.

Kurtosis g atsitiktinis dydis x apibrėžiamas lygybe .

Normalus skirstinys natūraliai turi g = 0. Jei g (x) > 0, tai reiškia, kad tikimybės tankio grafikas p x(x) yra labiau „paaštrintas“ nei normalusis pasiskirstymas, jei g (x)< 0, то “заостренность” графикаp x(x) yra mažesnis nei normaliojo skirstinio.

22. Binominio skirstinio dėsnis.

P yra įvykio tikimybė per vieną bandymą.
q – tikimybė, kad įvykis neįvyks per vieną bandymą q = (1-p)
n – testų skaičius
k – numatomas norimo įvykio įvykių skaičius
Bernulio formulė leidžia apskaičiuoti tikimybę, kad įvykis pasirodys n bandymų tiksliai k kartų.

23. Atsitiktinio dydžio normaliojo skirstinio dėsnis. Laplaso-Lyapunovo teorija.
Normalus (Gauso) skirstinys
Tai yra pagrindinis tikimybių teorijos dėsnis. Riboje visi dėsniai linkę į normalaus pasiskirstymo dėsnius. Begalinio skaičiaus atsitiktinių dydžių suma, paskirstyta pagal bet kokius dėsnius, galiausiai įgyja normalųjį pasiskirstymo dėsnį.

Ištisinis atsitiktinis dydis X vadinamas normaliai paskirstytu, jei jo pasiskirstymo tankis yra lygus:

– Matematinis lūkestis diskretinis atsitiktinis dydis yra atsitiktinio dydžio galimų dydžių sandaugų ir jų atsiradimo tikimybės suma

Sklaida- įvertinti kurio nors rodiklio sklaidos laipsnį (nukrypimą) nuo jo vidutinės reikšmės, vartojamos sklaidos sąvokos.

Imties dispersija arba atrankos dispersija yra kintamojo kintamumo matas. Nuokrypis apskaičiuojamas pagal formulę:

kur x yra imties vidurkis, N yra stebėjimų skaičius imtyje. Dispersija svyruoja nuo nulio iki begalybės. Kraštutinė reikšmė 0 reiškia, kad kintamumo nėra, kai kintamojo reikšmės yra pastovios. - atsitiktinio dydžio standartinis nuokrypis (kvadratinė dispersijos šaknis).

Normaliojo pasiskirstymo funkcijos grafikas, kaip matyti iš paveikslo, yra kupolo formos kreivės, vadinamos
Gauso, maksimalus taškas turi koordinates Tai reiškia, kad ši ordinatė mažėja didėjant reikšmei (kreivė „susispaudžia“ link Ox ašies) ir didėja mažėjant (kreivė „tempia“ teigiama Oy ašies kryptimi). Parametro u reikšmių keitimas (su pastovia verte) neturi įtakos kreivės formai, o tik perkelia kreivę išilgai Ox ašies. Normalus skirstinys su parametrais =0 ir =1 vadinamas normalizuotu. Atsitiktinio dydžio paskirstymo funkcija šiuo atveju bus tokia:

Jei =0, =1, grafikas įgauna tokią formą:

Ši kreivė ties =0, =1 gavo standarto statusą, ji vadinama vienetine normaliąja kreive, tai yra, bet kokius surinktus duomenis siekiama transformuoti taip, kad jų pasiskirstymo kreivė būtų kuo artimesnė šiai standartinei kreivei.

Normalizuota kreivė buvo išrasta siekiant išspręsti tikimybių teorijos problemas, tačiau praktiškai paaiškėjo, kad ji puikiai atitinka dažnio pasiskirstymą daugeliui daugelio kintamųjų.

Tegul x 1 , x 2 , …, x n , … yra neribota nepriklausomų atsitiktinių dydžių seka su matematiniais lūkesčiais m 1 , m 2 , …, m n , … ir dispersijos s 1 2 , s 2 2 , …, s n 2 … . Pažymime , ir .