Centrul de greutate al unui corp rigid și metode de găsire a poziției acestuia. Centrul de masă al corpului. Echilibru. Masa corporală Cum se numește centrul de greutate al unui corp solid?
Să selectăm un volum elementar dV=dx dy dz într-un solid neomogen (Fig. 5.3). Greutatea elementului selectat va fi , unde - gravitație specificăîntr-un punct al corpului cu coordonatele corespunzătoare.
Greutățile elementelor formează un sistem de forțe, paralel cu axa aplica Modulul rezultat
Greutățile elementului se numește greutate solid, iar punctul geometric de aplicare al rezultantei este centrul de greutate corp solid. Pentru a calcula aceste mărimi, folosim formulele (5.1) și (5.4), înlocuind însumarea în ele cu integrarea în volum, adică
Mărimea din numărătorul formulei (5.8) se numește momentul static al greutății unui corp rigid față de planul de coordonate.
Evident, pentru un corp omogen, formula (5.8) ia forma
Structura formulelor pentru calcule este similară.
În acest caz, centrul de greutate al corpului solid coincide cu centrul volumului său.
Dacă una dintre dimensiunile unui corp solid este semnificativ mai mică decât celelalte două, se numește corpul suprafata grea. Cu o greutate constantă pe unitatea de suprafață, este omogen. Formulele de calcul a greutății și coordonatele centrului de greutate se obțin din (5.7) – (5.9) prin înlocuirea integralelor peste volum cu integrale peste suprafață. În unele cazuri, suprafața poate fi plană.
Dacă două dimensiuni ale unui corp solid sunt semnificativ mai mici decât a treia, se numește corpul linie grea. Cu o greutate constantă pe unitatea de lungime a liniei, este omogenă. Formulele de calcul a greutății și coordonatele centrului de greutate se obțin din (5.7) – (5.9) prin înlocuirea integralelor de volum cu integrale curbilinii. În unele cazuri, linia poate fi dreaptă.
Dacă un corp solid omogen are un plan de simetrie, atunci centrul de greutate al corpului se află în acest plan (suma momentelor statice ale forțelor elementare de greutate în raport cu planul de simetrie este zero).
Dacă un corp solid omogen are două plane de simetrie, atunci centrul de greutate al corpului aparține liniei de intersecție a acestor plane.
Dacă un corp solid omogen are trei plane de simetrie, atunci centrul de greutate al corpului este situat în punctul de intersecție a acestora.
Dacă un corp rigid poate fi împărțit mental în elemente ale căror greutăți și poziții ale centrelor de greutate sunt cunoscute, atunci greutatea corpului rigid și poziția centrului său de greutate pot fi calculate folosind formulele (5.1) și (5.4). De exemplu, se calculează greutatea și coordonatele centrului de greutate al unei nave în construcție.
Dacă corpul are decupaje, atunci acestea pot fi considerate ca elemente de greutate negative.
Rețineți că în literatura de referință inginerească există un număr destul de mare de elemente omogene (volumerice, plate și curbate), pentru care se calculează greutățile și pozițiile centrelor de greutate. Tabelul de mai jos prezintă câteva dintre ele.
| Tipul elementului | Volumul (aria) elementului | Abscisa c.t. | ordonata c.t. | Aplicata c.t. |
În unele situații, poziția centrului de greutate al unui corp rigid poate fi găsită din rezultatele experimentului. De exemplu, atunci când atârnați un corp pe un fir, centrul său de greutate este situat pe linia firului. Atârnând corpul de un alt punct care nu se află pe prima linie, găsim poziția centrului de greutate al corpului ca punct de intersecție a două linii. O altă metodă folosită pentru a găsi centrul de greutate al corpurilor extinse este așa-numita plasare a acestuia pe „cuțite” cu lame paralele. Când „cuțitele” se unesc, centrul de greutate al corpului tinde să rămână între ele și, în limită, ajunge pe linia coincidenței lamelor.
În practica ingineriei, metodele care sunt o combinație de calcul și experiment pot fi utilizate pentru a determina poziția centrului de greutate al unui corp. Ca exemplu, să dăm calculul distanței centrului de greutate al aeronavei, prezentat în Fig. 5.4., de la roata sa din față.
În figură: D este un dinamometru care arată mărimea forței normale de presiune a roții din față, P este greutatea aeronavei, este distanța de la roata din față la axa roților din spate.
Evident, distanța de interes de la roata din față până la linia forței de greutate a avionului poate fi obținută din ecuația sumei momentelor de forță și P în jurul axei roților din spate, ca
Notă: dacă greutatea P a aeronavei nu este cunoscută, atunci prin deplasarea dinamometrului D sub roțile din spate, puteți obține valoarea forței normale de presiune. Apoi
Exemplul 5.1. Pentru o placă omogenă care are forma unui sector circular cu un unghi de 2 la vârf (vezi Fig. 5.5), găsiți poziția centrului de greutate al plăcii.
Să desenăm axa x astfel încât să fie bisectoarea unghiului 2. Apoi, din cauza simetriei, ordonata centrului de greutate este egală cu zero, adică. .
Folosind două raze, unghiul elementar între care este , selectăm un element de pe placă a cărui zonă este aproximativ egală cu aria unui triunghi isoscel
Abscisa centrului de greutate al elementului triunghiular selectat este egală cu .
Acum putem construi o expresie pentru calcularea abscisei centrului de greutate al unui sector circular ca
Notă: în timpul calculului s-a ținut cont de faptul că centrul de greutate al unui corp plat omogen are aceleași coordonate pe plan ca cele ale figurii plane corespunzătoare.
Exemplul 5.2. Pentru o placă subțire omogenă de formă complexă, ale cărei dimensiuni sunt indicate în Fig. 5.6, găsiți poziția centrului de greutate.
Să împărțim mental placa în trei elemente: un dreptunghi, un triunghi și un cerc. Pentru fiecare dintre elemente, găsim aria și coordonatele centrului de greutate:
Apoi, pentru placă, coordonatele centrului de greutate pot fi calculate folosind formulele:
La calcul, gaura a fost tratată ca atașarea unui cerc cu greutate negativă.
Centrul de greutate al unui corp solid este un punct geometric care este legat rigid de acest corp și este centrul forțelor gravitaționale paralele aplicate particulelor elementare individuale ale corpului (Figura 1.6).
Vector raza acestui punct

Figura 1.6
Pentru un corp omogen, poziția centrului de greutate al corpului nu depinde de material, ci este determinată de forma geometrică a corpului.
Dacă greutatea specifică a unui corp omogen γ , greutate particulă elementară corp
P k = yΔV k (P = γV ) înlocuiți în formula pentru a determina r C , avem
De unde, proiectand pe axe si trecand la limita, obtinem coordonatele centrului de greutate al unui volum omogen.

În mod similar pentru coordonatele centrului de greutate al unei suprafețe omogene cu arie S (Figura 1.7, a)


Figura 1.7
Pentru coordonatele centrului de greutate al unei linii omogene de lungime L (Figura 1.7, b)

Metode de determinare a coordonatelor centrului de greutate
Pe baza formulelor generale obținute mai devreme, putem indica metode pentru determinarea coordonatelor centrelor de greutate ale corpurilor solide:
1 Analitic(prin integrare).
2 Metoda simetriei. Dacă un corp are un plan, o axă sau un centru de simetrie, atunci centrul său de greutate se află, respectiv, în planul de simetrie, axa de simetrie sau centrul de simetrie.
3 Experimental(metoda de agățare a corpului).
4 Despicare. Corpul este împărțit într-un număr finit de părți, pentru fiecare dintre ele poziția centrului de greutate C si zona S cunoscut. De exemplu, proiecția unui corp pe un plan xOy (Figura 1.8) poate fi reprezentat ca două figuri plate cu zone S 1 Și S 2 (S=S 1 +S 2 ). Centrele de greutate ale acestor figuri sunt situate în puncte C 1 (X 1 , y 1 ) Și C 2 (X 2 , y 2 ) . Atunci coordonatele centrului de greutate al corpului sunt egale


Figura 1.8
5Plus(metoda suprafețelor sau volumelor negative). Un caz special al metodei de partiționare. Se aplică corpurilor care au decupaje dacă sunt cunoscute centrele de greutate ale corpului fără decupaj și partea decupată. De exemplu, trebuie să găsiți coordonatele centrului de greutate al unei figuri plate (Figura 1.9):


Figura 1.9
Centrele de greutate ale celor mai simple figuri

Figura 1.10
1 Triunghi
Centrul de greutate al ariei triunghiului coincide cu punctul de intersecție al medianelor sale (Figura 1.10, a).
DM = MB , CM= (1/3)A.M. .
2 Arc de cerc
Arcul are o axă de simetrie (Figura 1.10, b). Centrul de greutate se află pe această axă, adică y C = 0 .

dl – element arc, dl = Rdφ , R – raza cercului, x = Rcosφ , L= 2αR ,
Prin urmare:
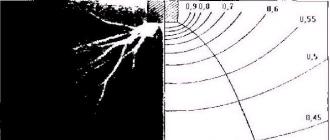
X C = R(sinα/α) .
3 Sector circular
Sectorul de rază R cu unghi central 2 α are o axă de simetrie Bou , pe care se află centrul de greutate (Figura 1.10, c).
Împărțim sectorul în sectoare elementare, care pot fi considerate triunghiuri. Centrele de greutate ale sectoarelor elementare sunt situate pe un arc de cerc de rază (2/3) R .
Centrul de greutate al sectorului coincide cu centrul de greutate al arcului AB :
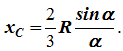
14. Metode de precizare a mișcării unui punct.
Cu metoda vectorială de specificare a mișcării, poziția unui punct este determinată de un vector cu rază desenat dintr-un punct fix în sistemul de referință selectat.
Cu metoda coordonatelor de specificare a mișcării, coordonatele unui punct sunt specificate în funcție de timp:

Acestea sunt ecuații parametrice ale traiectoriei unui punct în mișcare, în care timpul joacă rolul unui parametru t . Pentru a-și scrie ecuația în formă explicită, este necesar să excludem din ele t .
Cu metoda naturală de specificare a mișcării, se specifică traiectoria punctului, originea referinței pe traiectorie care indică direcția pozitivă a referinței și legea modificării coordonatei arcului: s=s(t) . Această metodă este convenabilă de utilizat dacă traiectoria punctului este cunoscută dinainte.
15. 1.2 Viteza punctului
Luați în considerare mișcarea unui punct pe o perioadă scurtă de timp Δt :
![]()
viteza medie a unui punct într-o perioadă de timp Dt . Viteza unui punct la un moment dat


Viteza punctului este o măsură cinematică a mișcării sale, egală cu derivata în timp a vectorului rază a acestui punct din sistemul de referință luat în considerare. Vectorul viteză este direcționat tangențial la traiectoria punctului în direcția mișcării.
Centrul de greutate al unui corp rigid
Centrul de greutate al unui corp solid este un punct geometric care este legat rigid de acest corp și este centrul forțelor gravitaționale paralele aplicate particulelor elementare individuale ale corpului (Figura 1.6).
Vector raza acestui punct

Figura 1.6
Pentru un corp omogen, poziția centrului de greutate al corpului nu depinde de material, ci este determinată de forma geometrică a corpului.
Dacă greutatea specifică a unui corp omogen γ , greutatea unei particule elementare a unui corp
P k = γΔV k (P = γV)
înlocuiți în formula pentru a determina r C , avem
De unde, proiectand pe axe si trecand la limita, obtinem coordonatele centrului de greutate al unui volum omogen.

În mod similar pentru coordonatele centrului de greutate al unei suprafețe omogene cu arie S (Figura 1.7, a)


Figura 1.7
Pentru coordonatele centrului de greutate al unei linii omogene de lungime L (Figura 1.7, b)

Metode de determinare a coordonatelor centrului de greutate
Pe baza formulelor generale obținute mai devreme, putem indica metode pentru determinarea coordonatelor centrelor de greutate ale corpurilor solide:

Figura 1.8

Figura 1.9
11. Concepte de bază ale cinematicii. Cinematica unui punct. Metode de precizare a mișcării unui punct. Viteza și accelerația unui punct.
Concepte de bază ale cinematicii
Cinematică- o ramură a mecanicii care studiază mișcarea corpurilor fără a ține cont de motivele care au determinat această mișcare.
Sarcina principală a cinematicii este să găsească poziția unui corp în orice moment dacă poziția, viteza și accelerația acestuia la momentul inițial sunt cunoscute.
Mișcare mecanică- aceasta este o schimbare a poziției corpurilor (sau părților corpului) unele față de altele în spațiu în timp.
Pentru a descrie mișcarea mecanică, este necesar să alegeți un sistem de referință.
Corp de referință- un corp (sau grup de corpuri), luat în acest caz ca nemișcat, în raport cu care se consideră mișcarea altor corpuri.
Sistem de referință- acesta este sistemul de coordonate asociat corpului de referință și metoda aleasă de măsurare a timpului (Fig. 1).

Poziția corpului poate fi determinată folosind vectorul rază r⃗ r→ sau folosind coordonatele.
Vector rază r⃗ r→ puncte Μ - un segment de dreaptă direcționat care leagă originea DESPRE cu un punct Μ (Fig. 2).

Coordona x puncte Μ este proiecția capătului vectorului rază al punctului Μ pe axă Oh. De obicei se folosește un sistem de coordonate dreptunghiular. În acest caz, poziția punctului Μ pe o linie, planul și, respectiv, în spațiu sunt determinate de unul ( X), Două ( X, la) și trei ( X, la, z) numere - coordonate (Fig. 3).

Într-un curs elementar, fizicienii studiază cinematica mișcării unui punct material.
Punct material- un corp ale cărui dimensiuni pot fi neglijate în condiții date.
Acest model este utilizat în cazurile în care dimensiunile liniare ale corpurilor luate în considerare sunt mult mai mici decât toate celelalte distanțe dintr-o problemă dată sau când corpul se mișcă translațional.
Progresist este mișcarea unui corp în care o linie dreaptă care trece prin oricare două puncte ale corpului se mișcă în timp ce rămâne paralelă cu ea însăși. În timpul mișcării de translație, toate punctele corpului descriu aceleași traiectorii și în orice moment au aceleași viteze și accelerații. Prin urmare, pentru a descrie o astfel de mișcare a unui corp, este suficient să descrieți mișcarea unui punct arbitrar.
În cele ce urmează, cuvântul „corp” va fi înțeles ca „punct material”.
Se numește linia pe care o descrie un corp în mișcare într-un anumit cadru de referință traiectorie. În practică, forma traiectoriei este specificată folosind formule matematice ( y = f(X) - ecuația traiectoriei) sau reprezentată în figură. Tipul de traiectorie depinde de alegerea sistemului de referință. De exemplu, traiectoria unui corp care căde liber într-un cărucior care se mișcă uniform și rectiliniu este o linie verticală dreaptă în cadrul de referință asociat cu căruciorul și o parabolă în cadrul de referință asociat cu Pământul.
În funcție de tipul de traiectorie, se disting mișcarea rectilinie și curbilinia.
cale s- o mărime fizică scalară determinată de lungimea traiectoriei descrisă de corp într-o anumită perioadă de timp. Calea este întotdeauna pozitivă: s > 0.
In miscareΔr⃗ Δr→ al unui corp pentru o anumită perioadă de timp - un segment de linie dreaptă direcționată care leagă inițialul (punctul M 0) și final (punct M) poziția corpului (vezi Fig. 2):
Δr⃗ =r⃗ −r⃗ 0, Δr→=r→−r→0,
unde r⃗ r→ și r⃗ 0 r→0 sunt vectorii de rază ai corpului în aceste momente de timp.
Proiecția mișcării pe axă Bou
Δrx=Δx=x−x0 Δrx=Δx=x−x0
Unde X 0 și X- coordonatele corpului în momentele inițiale și finale ale timpului.
Modulul de călătorie nu poate fi mai mare decât calea
|Δr⃗ |≤s |Δr→|≤s
Semnul egal se referă la cazul mișcării rectilinie, dacă direcția de mișcare nu se schimbă.
Cunoscând deplasarea și poziția inițială a corpului, puteți găsi poziția acestuia la momentul t:
r⃗ =r⃗ 0+Δr⃗ ; r→=r→0+Δr→;
(x=x0+Δrx;y=y0+Δry. (x=x0+Δrx;y=y0+Δry.
Viteză
Viteza medie hυ⃗ i hυ→i este o mărime fizică vectorială, numeric egală cu raportul dintre mișcare și perioada de timp în care a avut loc și direcționată de-a lungul mișcării (Fig. 4):
hυ⃗ i=Δr⃗ Δt;hυ⃗ i⇈Δr⃗ . hυ→i=Δr→Δt;hυ→i⇈Δr→.

Unitatea SI a vitezei este metru pe secundă (m/s).
Viteza medie găsită folosind această formulă caracterizează mișcarea doar pe acea secțiune a traiectoriei pentru care este determinată. Pe altă parte a traiectoriei poate fi diferit.
Uneori folosesc viteza medie
hυi=sΔt hυi=sΔt
Unde s este calea parcursă pe o perioadă de timp Δ t. Viteza medie a unei căi este o mărime scalară.
Viteza instantaneeυ⃗ υ→ a corpului - viteza corpului la un moment dat de timp (sau la un punct dat al traiectoriei). Este egală cu limita la care tinde viteza medie pe o perioadă infinitezimală de timp υ⃗ =limΔt→0Δr⃗ Δt=r⃗ ′ υ→=limΔt→0Δr→Δt=r→ ′. Aici r⃗ ′ r→ ′ este derivata vectorului rază în raport cu timpul.
În proiecție pe axă Oh:
υx=limΔt→0ΔxΔt=x′. υx=limΔt→0ΔxΔt=x′.
Viteza instantanee a corpului este direcționată tangențial la traiectorie în fiecare punct din direcția de mișcare (vezi Fig. 4).
Accelerare
Accelerație medie- o mărime fizică egală numeric cu raportul dintre schimbarea vitezei și timpul în care a avut loc:
ha⃗ i=Δυ⃗ Δt=υ⃗ −υ⃗ 0Δt. ha→i=Δυ→Δt=υ→−υ→0Δt.
Vectorul ha⃗ i ha→i este îndreptat paralel cu vectorul de schimbare a vitezei Δυ⃗ Δυ→ (ha⃗ i⇈Δυ⃗ ha→i⇈Δυ→) spre concavitatea traiectoriei (Fig. 5).

Accelerație instantanee:
a⃗ =limΔt→0Δυ⃗ Δt=υ⃗′. a→=limΔt→0Δυ→Δt=υ→ ′.
Unitatea SI a accelerației este metru pe secundă pătrat (m/s2).
În general, accelerația instantanee este direcționată la un unghi față de viteza. Cunoscând traiectoria, puteți determina direcția vitezei, dar nu și accelerația. Direcția accelerației este determinată de direcția forțelor rezultante care acționează asupra corpului.
În mișcare rectilinie cu o viteză care crește în valoare absolută (Fig. 6, a), vectorii a⃗ a→ și υ⃗ 0 υ→0 sunt codirecționali (a⃗ ⇈υ⃗ 0 a→⇈υ→0) iar proiecția accelerației pe direcția de mișcare este pozitivă.
În mișcare rectilinie cu viteză descrescătoare (Fig. 6, b), direcțiile vectorilor a⃗ a→ și υ⃗ 0 υ→0 sunt opuse (a⃗ ↓υ⃗ 0 a→↓υ→0) iar proiecția accelerației pe direcția de mișcare este negativă.
Vectorul a⃗ a→ în timpul mișcării curbilinie poate fi descompus în două componente direcționate de-a lungul vitezei a⃗ τ a→τ și perpendicular pe viteza a⃗ n a→n (Fig. 1.7), a⃗ τ a→τ este accelerația tangențială, care caracterizează viteza de modificare a modulului vitezei în timpul mișcării curbilinie, a⃗ n a→n - accelerație normală, care caracterizează viteza de schimbare a direcției vectorului viteză în timpul mișcării curbilinie Modulul de accelerație a=a2τ+a2n−−−−−−√ a=aτ2 +an2.

Metode pentru specificarea mișcării punctului
Pentru a specifica mișcarea unui punct, puteți utiliza una dintre următoarele trei metode:
1) vector, 2) coordonate, 3) natural.
1. Metoda vectoriala de precizare a miscarii unui punct.
Lasă punctul M se mișcă în raport cu un anumit cadru de referință Oxyz. Poziția acestui punct în orice moment poate fi determinată prin specificarea vectorului său de rază trasat de la origine DESPRE exact M(Fig. 3).

Fig.3
Când punctul se mișcă M vectorul se va schimba în timp atât ca mărime, cât și ca direcție. Prin urmare, este un vector variabil (vector funcție) în funcție de argumentul t:
Egalitatea definește legea de mișcare a unui punct în formă vectorială, deoarece ne permite să construim un vector corespunzător în orice moment și să găsim poziția punctului în mișcare.
Locația geometrică a capetelor vectorului, i.e. odograf acest vector determină traiectoria punctului în mișcare.
2. Metoda coordonatelor de precizare a mișcării unui punct.
Poziția unui punct poate fi determinată direct de coordonatele sale carteziene x, y, z(Fig. 3), care se va schimba în timp pe măsură ce punctul se mișcă. Pentru a cunoaște legea mișcării unui punct, adică poziția sa în spațiu în orice moment în timp, trebuie să cunoașteți coordonatele punctului pentru fiecare moment în timp, adică. cunoaște dependențele
x=f 1 (t), y=f 2 (t), z=f 3 (t).
Ecuațiile sunt ecuațiile de mișcare ale unui punct în coordonate carteziene dreptunghiulare. Ei determină legea mișcării unui punct folosind metoda coordonatelor de specificare a mișcării.
Pentru a obține ecuația traiectoriei, este necesar să excludem parametrul t din ecuațiile de mișcare.
Nu este dificil să se stabilească o relație între metodele vectoriale și coordonate de specificare a mișcării.
Să descompunăm vectorul în componente de-a lungul axelor de coordonate:
![]()
unde r x , ry y , r z - proiecții ale vectorului pe axă; – vectori unitari dirijati de-a lungul axelor, vectori unitari ai axelor.
Deoarece originea vectorului este la originea coordonatelor, proiecțiile vectorului vor fi egale cu coordonatele punctului M. De aceea
Dacă mișcarea punctului este specificată în coordonate polare
r=r(t), φ = φ(t),
unde r este raza polară, φ este unghiul dintre axa polară și raza polară, atunci aceste ecuații exprimă ecuația traiectoriei unui punct. Eliminând parametrul t, obținem
r = r(φ).
Exemplul 1. Mișcarea unui punct este dată de ecuații

Fig.4
Pentru a exclude timpul, parametrul t, găsim din prima ecuație sin2t=x/2, din a doua cos2t=y/3. Apoi pătrați și adăugați-l. Deoarece sin 2 2t+cos 2 2t=1, obținem . Aceasta este ecuația unei elipse cu semi-axe de 2 cm și 3 cm (Fig. 4).
Poziția punctului de pornire M 0 (la t=0) este determinată de coordonatele x 0 =0, y 0 =3 cm.
După 1 sec. punctul va fi pe poziție M 1 cu coordonatele
x 1 =2sin2=2∙0,91=1,82 cm, y 1 =2cos2=3∙(-0,42)= -1,25 cm.
Notă.
Mișcarea unui punct poate fi specificată folosind alte coordonate. De exemplu, cilindric sau sferic. Printre acestea vor fi nu numai dimensiuni liniare, ci și unghiuri. Dacă este necesar, vă puteți familiariza cu specificarea mișcării folosind coordonatele cilindrice și sferice din manuale.
3. O modalitate naturală de a specifica mișcarea unui punct.

Fig.5
Modul natural de specificare a mișcării este convenabil de utilizat în cazurile în care traiectoria unui punct în mișcare este cunoscută dinainte. Lasă curba AB este traiectoria punctului M când se deplasează în raport cu sistemul de referinţă Oxyz(Fig. 5) Să alegem un punct fix pe această traiectorie DESPRE", pe care o luăm ca origine a referinței și setăm direcțiile de referință pozitive și negative pe traiectorie (ca pe axa de coordonate).
Apoi poziția punctului M pe traiectorie va fi determinată în mod unic de coordonatele curbilinii s, care este egală cu distanța de la punct DESPRE' până la punctul M, măsurată de-a lungul arcului traiectoriei și luată cu semnul corespunzător. La mutarea punctului M se mută pe poziții M 1 , M 2,... . deci distanta s se va schimba în timp.
Pentru a cunoaște poziția unui punct M pe traiectorie în orice moment, trebuie să cunoașteți dependența
Ecuația exprimă legea mișcării unui punct M de-a lungul traiectoriei. Funcția s= f(t) trebuie să fie unică, continuă și diferențiabilă.
Direcția pozitivă de referință a coordonatei arcului s se consideră a fi direcția de mișcare a punctului în momentul în care acesta ocupă poziția O. Trebuie reținut că ecuația s=f(t) nu determină legea mișcării a punctului în spațiu, deoarece pentru a determina poziția punctului în spațiu trebuie să cunoașteți traiectoria unui punct cu poziția inițială a punctului pe el și o direcție pozitivă fixă. Astfel, mișcarea unui punct este considerată dată în mod natural dacă se cunosc traiectoria și ecuația (sau legea) mișcării punctului de-a lungul traiectoriei.
Este important de remarcat faptul că coordonata arcului punctului s este diferită de calea σ parcursă de punctul de-a lungul traiectoriei. În timpul mișcării sale, un punct parcurge o anumită cale σ, care este funcție de timpul t. Cu toate acestea, distanța parcursă σ coincide cu distanța s numai atunci când funcția s = f(t) se modifică monoton cu timpul, adică. când un punct se mișcă într-o direcție. Să presupunem că punctul M se deplasează de la M 1 la M 2. Poziția punctului în M 1 corespunde timpului t 1, iar poziția punctului în M 2 corespunde timpului t 2. Să descompunăm intervalul de timp t 2 - t 1 în intervale de timp foarte mici ∆t 1 (i = 1,2, ...n) astfel încât în fiecare dintre ele punctul să se miște într-o direcție. Să notăm incrementul corespunzător al coordonatei arcului ca ∆s i . Calea σ parcursă de punct va fi o valoare pozitivă:

Dacă mișcarea unui punct este specificată prin metoda coordonatelor, atunci calea parcursă este determinată de formulă

unde dx=xdt, dy= ydt, dz=zdt.
Prin urmare,
Exemplul 2. Punctul se deplasează în linie dreaptă, conform legii s=2t+3 (cm) (Fig. 6).

Fig.6
La inceputul miscarii, la t=0 s=OM 0 =s 0 =3 cm.Pozitia punctului M 0 este numit pozitia de pornire. La t=1 s, s=OM1 =5 cm.
Desigur, în 1 secundă. punctul a parcurs distanța M 0 M 1 = 2 cm Deci s– aceasta nu este calea parcursă de punct, ci distanța de la origine până la punct.
Vector viteza punctului
Una dintre principalele caracteristici cinematice ale mișcării unui punct este o mărime vectorială numită viteza punctului. Conceptul de viteză a unui punct în mișcare rectilinie uniformă este unul dintre conceptele elementare.
Viteză- o măsură a stării mecanice a corpului. Caracterizează viteza de schimbare a poziției corpului față de un sistem de referință dat și este o mărime fizică vectorială.
Unitatea de măsură a vitezei este m/s. Alte unități sunt adesea folosite, de exemplu, km/h: 1 km/h=1/3,6 m/s.
Mișcarea unui punct se numește uniformă dacă incrementele vectorului rază a punctului pe perioade egale de timp sunt egale între ele. Dacă traiectoria punctului este o linie dreaptă, atunci mișcarea punctului se numește rectilinie.
Pentru o mișcare uniformă liniară
∆r= v∆t, (1)
Unde v– vector constant.
Vector v numită viteza mișcării rectilinie și uniforme o determină complet.
Din relația (1) reiese clar că viteza mișcării rectilinie și uniforme este o mărime fizică care determină mișcarea unui punct pe unitatea de timp. Din (1) avem
Direcția vectorială v indicat în fig. 6.1.

Fig.6.1
Pentru mișcarea neuniformă, această formulă nu este potrivită. Să introducem mai întâi conceptul de viteză medie a unui punct pe o anumită perioadă de timp.
Lăsați punctul de mișcare să fie în momentul de timp t gravidă M, determinată de vectorul rază, iar în momentul t 1 vine pe poziție M 1 definit de un vector (Fig. 7). Atunci mișcarea punctului în perioada de timp ∆t=t 1 -t este determinată de un vector pe care îl vom numi vector de mișcare a punctului. Dintr-un triunghi OMM 1 este clar că ; prin urmare,

Orez. 7
Raportul dintre vectorul de mișcare al unui punct și perioada de timp corespunzătoare dă o mărime vectorială numită viteza medie a punctului în valoare absolută și direcție pe perioada de timp ∆t:
Viteza unui punct la un moment dat t este mărimea vectorială v la care tinde viteza medie v cf pe măsură ce intervalul de timp ∆t tinde spre zero:
Deci, vectorul viteză al unui punct la un moment dat este egal cu prima derivată a vectorului rază a punctului în raport cu timpul.
Deoarece sensul limitativ al secantei MM 1 este o tangentă, atunci vectorul viteză al punctului la un moment dat este direcționat tangent la traiectoria punctului în direcția mișcării.
Determinarea vitezei unui punct folosind metoda coordonatelor de specificare a mișcării
Vectorul viteză punctual, ținând cont de faptul că r x =x, r y =y, r z =z, găsim:
![]()
Astfel, proiecția vitezei punctului pe axele de coordonate sunt egale cu primele derivate ale coordonatelor corespunzătoare ale punctului în raport cu timpul.
Cunoscând proiecțiile vitezei, vom găsi mărimea și direcția acesteia (adică unghiurile α, β, γ pe care le formează vectorul v cu axele de coordonate) folosind formulele
![]()
Deci, valoarea numerică a vitezei unui punct la un moment dat este egală cu prima derivată a distanței (coordonată curbilinie) s puncte în timp.
Vectorul viteză este direcționat tangențial la traiectorie, care ne este cunoscută dinainte.
Determinarea vitezei unui punct folosind metoda naturală de specificare a mișcării
Valoarea vitezei poate fi definită ca limită (∆r – lungimea coardei MM 1):
unde ∆s – lungimea arcului MM 1 . Prima limită este egală cu unitatea, a doua limită este derivata ds/dt.
În consecință, viteza unui punct este derivata pentru prima dată a legii mișcării:
Vectorul viteză este direcționat, așa cum sa stabilit mai devreme, tangent la traiectorie. Dacă valoarea vitezei la un moment dat este mai mare decât zero, atunci vectorul viteză este direcționat într-o direcție pozitivă
Vector de accelerație punctual
Accelerare- mărime fizică vectorială care caracterizează viteza de schimbare a vitezei. Acesta arată cât de mult se modifică viteza unui corp pe unitatea de timp.
Unitatea SI a accelerației este metru pe secundă pătrat. la intervalul de timp corespunzător ∆t determină vectorul accelerației medii a punctului în această perioadă de timp:
Vectorul de accelerație medie are aceeași direcție ca vectorul, adică. îndreptată spre concavitatea traiectoriei.
Accelerația unui punct la un moment dat t se numește mărime vectorială la care tinde accelerația medie pe măsură ce intervalul de timp ∆t tinde spre zero: Vectorul accelerație al unui punct la un moment dat este egal cu derivata întâi a vectorului viteză sau derivata a doua a vectorului rază a punctul cu privire la timp.
Accelerația unui punct este zero numai când viteza punctului v constantă atât ca mărime, cât și ca direcție: aceasta corespunde doar mișcării rectilinie și uniforme.
Să aflăm cum este situat vectorul în raport cu traiectoria punctului. În mișcare rectilinie, vectorul este îndreptat de-a lungul liniei drepte de-a lungul căreia se mișcă punctul. îndreptată spre concavitatea traiectoriei și se află în planul care trece prin tangenta la traiectorie în punctul Mși o dreaptă paralelă cu tangenta într-un punct adiacent M 1 (Fig. 8). În limita când punctul M se străduiește pentru M, acest plan ocupă poziţia aşa-numitului plan osculator, adică. planul în care are loc o rotație infinitezimală a tangentei la traiectorie în timpul unei mișcări elementare a unui punct în mișcare. Prin urmare, în cazul general, vectorul de accelerație se află în planul de contact și este îndreptat spre concavitatea curbei.
Determinarea accelerației folosind metoda coordonatelor de specificare a mișcării
Vectorul accelerație al unui punct în proiecție pe axă se obține:
acestea. proiecția accelerației unui punct pe axele de coordonate este egală cu primele derivate ale proiecțiilor vitezei sau cu derivatele secunde ale coordonatelor corespunzătoare ale punctului în raport cu timpul. Mărimea și direcția accelerației pot fi găsite din formule
Fig.10
Proiecții de accelerație a x = =0, a y = =-8 cm∙s -2. Din moment ce proiectia vectorului acceleratie pe axa X este egal cu zero și pe axă y– este negativ, atunci vectorul de accelerație este îndreptat vertical în jos, iar valoarea lui este constantă și nu depinde de timp.
Orice corp poate fi considerat ca o colecție de puncte materiale, care pot fi, de exemplu, luate ca molecule. Fie corpul format din n puncte materiale cu mase m1, m2, ...mn.
Centrul de masă al corpului, format din n puncte materiale se numește punct (în sens geometric), al cărui vector rază este determinat de formula:
Aici R1 este vectorul rază al punctului numărul i (i = 1, 2, ... n).
Această definiție pare neobișnuită, dar de fapt dă poziția chiar a centrului de masă, despre care avem o idee intuitivă. De exemplu, centrul de masă al tijei va fi în mijlocul acesteia. Suma maselor tuturor punctelor incluse în numitorul formulei de mai sus se numește masa corpului. Greutate corporala numit suma maselor tuturor punctelor sale: m = m1 + m2 + ... + mn.

În corpurile omogene simetrice, CM este întotdeauna situat în centrul de simetrie sau se află pe axa de simetrie dacă figura nu are un centru de simetrie. Centrul de masă poate fi situat atât în interiorul corpului (disc, pătrat, triunghi), cât și în exteriorul acestuia (inel, cadru, pătrat).
Pentru o persoană, poziția COM depinde de postura adoptată. În multe sporturi, o componentă importantă a succesului este capacitatea de a menține echilibrul. Deci, la gimnastică, acrobație
un număr mare de elemente vor include tipuri diferite echilibru. Abilitatea de a menține echilibrul este importantă patinaj artistic, la patinaj, unde suportul are o suprafata foarte mica.
Condițiile pentru echilibrul unui corp în repaus sunt egalitatea simultană cu zero a sumei forțelor și suma momentelor forțelor care acționează asupra corpului.
Să aflăm ce poziție ar trebui să ocupe axa de rotație pentru ca corpul fixat de ea să rămână în echilibru sub influența gravitației. Pentru a face acest lucru, să spargem corpul în multe bucăți mici și să desenăm forțele gravitaționale care acționează asupra lor.

În conformitate cu regula momentelor, pentru echilibru este necesar ca suma momentelor tuturor acestor forțe în jurul axei să fie egală cu zero.
Se poate arăta că pentru fiecare corp există un singur punct în care suma momentelor de greutate în jurul oricărei axe care trece prin acest punct este egală cu zero. Acest punct se numește centru de greutate (de obicei coincide cu centrul de masă).
Centrul de greutate al corpului (CG) numit punctul relativ la care suma momentelor gravitaționale care acționează asupra tuturor particulelor corpului este egală cu zero.
Astfel, forțele gravitaționale nu fac corpul să se rotească în jurul centrului de greutate. Prin urmare, toate forțele gravitaționale ar putea fi înlocuite cu o singură forță care este aplicată în acest punct și este egală cu forța gravitațională.
Pentru a studia mișcările corpului unui atlet, este adesea introdus termenul de centru de greutate general (GCG). Proprietățile de bază ale centrului de greutate:
Dacă corpul este fixat pe o axă care trece prin centrul de greutate, atunci forța de greutate nu îl va determina să se rotească;
Centrul de greutate este punctul de aplicare al gravitației;
Într-un câmp uniform, centrul de greutate coincide cu centrul de masă.
Echilibrul este o poziție a corpului în care poate rămâne în repaus atât timp cât se dorește. Când un corp se abate de la poziția sa de echilibru, forțele care acționează asupra lui se schimbă și echilibrul forțelor este perturbat.
Exista tipuri diferite echilibru (fig. 9). Se obișnuiește să se distingă trei tipuri de echilibru: stabil, instabil și indiferent.
Echilibrul stabil (Fig. 9, a) se caracterizează prin faptul că corpul revine la poziția inițială atunci când este deviat. În acest caz, apar forțe sau momente de forță, care tind să readucă corpul în poziția inițială. Un exemplu este poziția corpului cu suport superior (de exemplu, agățat de o bară transversală), când, cu orice abateri, corpul tinde să revină la poziția inițială.
Echilibrul indiferent (Fig. 9, b) se caracterizează prin faptul că atunci când poziția corpului se schimbă, nu apar forțe sau momente de forță care tind să readucă corpul în poziția inițială sau să îndepărteze în continuare corpul din acesta. Aceasta este o întâmplare rară la om. Un exemplu este starea de imponderabilitate pe o navă spațială.
Echilibrul instabil (Fig. 9, c) se observă atunci când, cu mici abateri ale corpului, apar forțe sau momente de forță care tind să devieze și mai mult corpul de la poziția inițială. Un astfel de caz poate fi observat atunci când o persoană, stând pe un suport de o zonă foarte mică (mult mai mică decât aria celor două picioare sau chiar a unui picior), se aplecă în lateral.
Figura 9. Echilibrul corpului: stabil (a), indiferent (b), instabil (c)

Alături de tipurile enumerate de echilibru al corpurilor, biomecanica ia în considerare un alt tip de echilibru - limitat-stabil. Acest tip de echilibru se distinge prin faptul că corpul se poate întoarce la poziția inițială atunci când se abate de la el la o anumită limită, de exemplu, determinată de limita zonei de sprijin. Dacă abaterea depășește această limită, echilibrul devine instabil.
Sarcina principală în asigurarea echilibrului corpului uman este să se asigure că proiecția GCM-ului corpului se află în zona de sprijin. În funcție de tipul de activitate (menținerea unei poziții statice, mers, alergare etc.) și cerințele de stabilitate, frecvența și viteza influențelor corective se modifică, dar procesele de menținere a echilibrului sunt aceleași.
Distribuția masei în corpul uman
Masa corporală și masele segmentelor individuale sunt foarte importante pentru diferite aspecte ale biomecanicii. În multe sporturi este necesar să se cunoască distribuția masei de produs tehnica corecta efectuarea de exerciții. Pentru a analiza mișcările corpului uman, se folosește metoda de segmentare: este disecat condiționat în anumite segmente. Pentru fiecare segment se determină masa acestuia și poziția centrului de masă. În tabel 1 masele părților corpului sunt determinate în unități relative.
Tabelul 1. Masele părților corpului în unități relative
Adesea, în locul conceptului de centru de masă, se folosește un alt concept - centrul de greutate. Într-un câmp uniform de greutate, centrul de greutate coincide întotdeauna cu centrul de masă. Poziția centrului de greutate al legăturii este indicată ca distanța sa față de axa articulației proximale și este exprimată în raport cu lungimea legăturii, luată ca unitate.
În tabel Figura 2 prezintă poziția anatomică a centrelor de greutate ale diferitelor părți ale corpului.
Masa 2. Centrele de greutate ale părților corpului
| Parte a corpului | Poziția centrului de greutate |
| Şold | 0,44 lungime link |
| Fluierul piciorului | 0,42 lungime link |
| Umăr | 0,47 lungime link |
| Antebraț | 0,42 lungime link |
| trunchi | |
| Cap | |
| Perie | |
| Picior | |
| Umăr | 0,47 lungime link |
| Antebraț | 0,42 lungime link |
| trunchi | 0,44 distanțe de la axa transversală a articulațiilor umărului la axa articulațiilor șoldului |
| Cap | Situat în zona selei turcice a osului sfenoid (proiecție din față între sprâncene, din lateral - 3,0 - 3,5 deasupra canalului auditiv extern) |
| Perie | În regiunea capului celui de-al treilea os metacarpian |
| Picior | Pe o linie dreaptă care leagă tuberculul calcanean al calcaneului cu capătul celui de-al doilea deget la o distanță de 0,44 de primul punct |
| Centrul de greutate general cu o poziție verticală a corpului | Situat in pozitia principala in zona pelviana, in fata sacrului |
Dacă un corp solid este situat lângă suprafața Pământului, atunci gravitația este aplicată fiecărui punct material al acestui corp. Mai mult, dimensiunile corpului sunt atât de mici în comparație cu dimensiunea Pământului încât forțele gravitaționale care acționează asupra tuturor particulelor corpului pot fi considerate paralele între ele.
Punctul central CU) se numește un sistem de forțe gravitaționale paralele în toate punctele corpului centrul de greutate al unui corp rigid , iar suma forțelor gravitaționale ale tuturor punctelor sale materiale se numește gravitatie , acţionând asupra lui
Coordonatele centrului de greutate al unui corp solid sunt determinate de formulele:
unde sunt coordonatele punctelor de aplicare a forţelor gravitaţionale asupra cărora acţionează k al-lea punct material.
Pentru un corp omogen:
unde V este volumul întregului corp;
V k- volum k--lea particule.
Pentru o placă subțire uniformă:
![]()
unde S este aria plăcii;
S k – pătrat k- o parte din farfurie.
Pentru linie:
Unde L- lungimea întregii linii;
Lk- lungime k-a parte a liniei.
Metode de determinare a coordonatelor centrelor de greutate ale corpurilor:
Teoretic
Simetrie. Dacă un corp omogen are un plan, o axă sau un centru de simetrie, atunci centrul său de greutate se află, respectiv, fie în planul de simetrie, fie pe axă, fie în centrul de simetrie.
Despicare. Dacă un corp poate fi împărțit într-un număr finit de astfel de părți, pentru fiecare dintre care poziția centrului de greutate este cunoscută, atunci coordonatele centrului de greutate al întregului corp pot fi calculate direct folosind formulele de mai sus.
Plus. Această metodă este un caz special al metodei de partiționare. Se aplică corpurilor care au decupaje dacă sunt cunoscute centrele de greutate ale corpului fără decupaj și partea decupată. Ele sunt incluse în calcule cu semnul „-”.
Integrare. Când un corp nu poate fi împărțit în părți componente ale căror centre de greutate sunt cunoscute, se folosește metoda de integrare, care este universală.
Experimental
Metoda de agățare. Corpul este suspendat din două sau trei puncte, desenând linii verticale din ele. Punctul de intersecție a acestora este centrul de masă.
Metoda de cântărire. Corp în diferite părți aşezate pe cântare, determinându-se astfel reacţiile de suport. Se întocmesc ecuații de echilibru, din care se determină coordonatele centrului de greutate.
 Prin utilizarea metode teoretice formule de determinare coordonatele centrului de greutate
cel mai comun corpuri omogene:
Prin utilizarea metode teoretice formule de determinare coordonatele centrului de greutate
cel mai comun corpuri omogene:
Arc de cerc