Cum să găsiți proiecțiile unui vector pe axele de coordonate. Vectori și operații pe vectori. Proprietăți de proiecție vectorială
Definiție 1. Pe un plan, o proiecție paralelă a punctului A pe axa l este un punct - punctul de intersecție al axei l cu o dreaptă trasă prin punctul A paralel cu vectorul care specifică direcția de proiectare.
Definiția 2. Proiecția paralelă a unui vector pe axa l (față de vector) este coordonata vectorului relativ la bază axa l, unde punctele și sunt proiecții paralele ale punctelor A și B pe axa l, respectiv (Fig. 1).
Conform definiţiei pe care o avem
Definiţia 3. dacă și pe baza axei l Carteziană, adică proiecția vectorului pe axa l numite ortogonale (Fig. 2).
În spațiu, definiția 2 a proiecției vectoriale pe axă rămâne în vigoare, doar direcția de proiecție este specificată de doi vectori necoliniari (Fig. 3).

Din definiția proiecției unui vector pe o axă rezultă că fiecare coordonată a unui vector este o proiecție a acestui vector pe axa definită de vectorul de bază corespunzător. În acest caz, direcția de proiectare este specificată de alți doi vectori de bază dacă proiectul este realizat (considerat) în spațiu, sau de un alt vector de bază dacă proiectul este considerat pe un plan (Fig. 4).

Teorema 1. Proiecția ortogonală a unui vector pe axa l este egală cu produsul dintre modulul vectorului și cosinusul unghiului dintre direcția pozitivă a axei l și, i.e.

Pe cealaltă parte
Din noi găsim
Înlocuind AC în egalitatea (2), obținem
Din moment ce numerele Xși același semn în ambele cazuri luate în considerare ((Fig. 5, a) ; (Fig. 5, b), apoi din egalitate (4) rezultă
Cometariu. În cele ce urmează, vom lua în considerare doar proiecția ortogonală a vectorului pe axă și, prin urmare, cuvântul „ort” (ortogonal) va fi omis din notație.
Să prezentăm o serie de formule care sunt folosite mai târziu în rezolvarea problemelor.
a) Proiecția vectorului pe axă.
Dacă, atunci proiecția ortogonală pe vector conform formulei (5) are forma
c) Distanța de la un punct la un plan.

Fie b un plan dat cu un vector normal, M un punct dat,
d este distanța de la punctul M la planul b (fig. 6).
Dacă N este un punct arbitrar al planului b și și sunt proiecții ale punctelor M și N pe axă, atunci
- G) Distanța dintre liniile care se intersectează.

Fie a și b drepte care se încrucișează, un vector perpendicular pe ele, A și B să fie puncte arbitrare ale dreptelor a și, respectiv, b (Fig. 7), și și să fie proiecții ale punctelor A și B pe, atunci
e) Distanța de la un punct la o dreaptă.
Lăsa l- o linie dreaptă dată cu un vector de direcție, M - un punct dat,
N - proiecția sa pe linie l, apoi - distanța necesară (Fig. 8).
Dacă A este un punct arbitrar pe o dreaptă l, apoi într-un triunghi dreptunghic MNA se pot găsi ipotenuza MA și catetele. Mijloace,

f) Unghiul dintre o dreaptă și un plan.

Fie vectorul de direcție al acestei linii l, - vector normal al unui plan dat b, - proiecția unei drepte l la planul b (Fig. 9).
După cum se știe, unghiul μ dintre o linie dreaptă l iar proiecția sa pe planul b se numește unghiul dintre linie și plan. Avem
Să dăm exemple de rezolvare a problemelor metrice folosind metoda coordonatelor vectoriale.
În primul rând, să ne amintim despre ce este vorba axa de coordonate, proiecția unui punct pe o axăȘi coordonatele unui punct de pe axă.
Axa de coordonate- Aceasta este o linie dreaptă căreia i se dă o anumită direcție. Vă puteți gândi la el ca un vector cu un modul infinit de mare.
Axa de coordonate notată cu o literă: X, Y, Z, s, t... De obicei, pe axă se selectează (arbitrar) un punct, care se numește origine și, de regulă, este notat cu litera O. Din acest punct, sunt măsurate distanțele până la alte puncte de interes pentru noi.
Proiectia unui punct pe o axa- aceasta este baza perpendicularei coborâte din acest punct către această axă (Fig. 8). Adică proiecția unui punct pe axă este un punct.
Coordonata punctului pe axa- acesta este numărul valoare absolută care este egală cu lungimea segmentului de axă (pe scara selectată) cuprins între originea axei și proiecția punctului pe această axă. Acest număr se ia cu semnul plus dacă proiecția punctului este situată în direcția axei de la origine și cu semnul minus dacă este în sens opus.
Proiecția scalară a unui vector pe o axă- Acest număr, a cărui valoare absolută este egală cu lungimea segmentului de axă (pe scara selectată) cuprinsă între proiecțiile punctului de început și punctul final al vectorului. Important! De obicei, în locul expresiei proiecția scalară a unui vector pe o axă pur și simplu spun - proiecția vectorului pe axă, adică cuvântul scalar coborât. Proiecție vectorială este notat cu aceeași literă cu vectorul proiectat (în scriere normală, fără caractere aldine), cu un index inferior (de regulă) al numelui axei pe care este proiectat acest vector. De exemplu, dacă un vector este proiectat pe axa X A, atunci proiecția sa se notează cu x. Când proiectați același vector pe o altă axă, de exemplu, axa Y, proiecția sa va fi notă cu y (Fig. 9).

A calcula proiecția vectorului pe axă(de exemplu, axa X), este necesar să se scadă coordonatele punctului de plecare din coordonatele punctului său final, adică
a x = x k − x n.
Trebuie să ne amintim: proiecția scalară a unui vector pe o axă (sau, pur și simplu, proiecția unui vector pe o axă) este un număr (nu un vector)! Mai mult, proiecția poate fi pozitivă dacă valoarea x k este mai mare decât valoarea x n, negativă dacă valoarea x k este mai mică decât valoarea x n și egală cu zero dacă x k este egal cu x n (Fig. 10).

Proiecția unui vector pe o axă poate fi găsită și cunoscând modulul vectorului și unghiul pe care îl formează cu această axă.
Din figura 11 este clar că a x = a Cos α
Adică, proiecția vectorului pe axă este egală cu produsul dintre modulul vectorului și cosinusul unghiului între direcția axei și direcția vectorului. Dacă unghiul este ascuțit, atunci Cos α > 0 și a x > 0, iar dacă este obtuz, atunci cosinusul unghiului obtuz este negativ, iar proiecția vectorului pe axă va fi și ea negativă.

Unghiurile măsurate de pe axa în sens invers acelor de ceasornic sunt considerate pozitive, iar unghiurile măsurate de-a lungul axei sunt negative. Totuși, deoarece cosinusul este o funcție pară, adică Cos α = Cos (− α), atunci când se calculează proiecțiile, unghiurile pot fi numărate atât în sensul acelor de ceasornic, cât și în sens invers acelor de ceasornic.
La rezolvarea problemelor se vor folosi adesea următoarele proprietăți ale proiecțiilor: dacă
A = b + c +…+ d, apoi a x = b x + c x +…+ d x (similar cu alte axe),
A= m b, apoi a x = mb x (în mod similar pentru alte axe).
Formula a x = a Cos α va fi De multe ori apar atunci când rezolvați probleme, așa că trebuie neapărat să o știți. Trebuie să cunoașteți regula pentru determinarea proiecției pe de rost!
Tine minte!
Pentru a găsi proiecția unui vector pe o axă, modulul acestui vector trebuie înmulțit cu cosinusul unghiului dintre direcția axei și direcția vectorului.
Încă o dată - pe de rost!
Introducere…………………………………………………………………………………………… 3
1. Valoarea vectorului și scalarului…………………………………………….4
2. Definirea proiecției, axei și coordonatei unui punct…………..5
3. Proiecția vectorului pe axă………………………………………………………………………6
4. Formula de bază a algebrei vectoriale………………………………………..8
5. Calculul modulului unui vector din proiecțiile sale……………9
Concluzie…………………………………………………………………………………….11
Literatura……………………………………………………………………………………….12
Introducere:
Fizica este indisolubil legată de matematică. Matematica oferă fizicii mijloacele și tehnicile pentru o exprimare generală și precisă a relației dintre mărimile fizice care sunt descoperite ca urmare a experimentului sau a cercetării teoretice La urma urmei, principala metodă de cercetare în fizică este experimentală. Aceasta înseamnă că un om de știință dezvăluie calcule folosind măsurători. Indică relația dintre diferitele mărimi fizice. Apoi, totul este tradus în limbajul matematicii. Format model matematic. Fizica este o știință care studiază cele mai simple și în același timp cele mai generale legi. Sarcina fizicii este de a crea în mintea noastră o imagine a lumii fizice care să reflecte cel mai pe deplin proprietățile acesteia și să asigure astfel de relații între elementele modelului care există între elemente.
Deci, fizica creează un model al lumii din jurul nostru și îi studiază proprietățile. Dar orice model este limitat. Atunci când se creează modele ale unui anumit fenomen, sunt luate în considerare numai proprietățile și conexiunile care sunt esențiale pentru o gamă dată de fenomene. Aceasta este arta unui om de știință - de a alege principalul lucru din toată diversitatea.
Modelele fizice sunt matematice, dar matematica nu este baza lor. Relațiile cantitative dintre mărimile fizice sunt determinate ca urmare a măsurătorilor, observațiilor și cercetare experimentalăși sunt exprimate doar în limbajul matematicii. Cu toate acestea, nu există un alt limbaj pentru a construi teorii fizice.
1. Înțelesul vectorului și scalarului.
În fizică și matematică, un vector este o mărime care se caracterizează prin valoarea și direcția sa numerică. În fizică, există multe cantități importante care sunt vectori, de exemplu, forța, poziția, viteza, accelerația, cuplul, impulsul, puterea câmpului electric și magnetic. Ele pot fi contrastate cu alte cantități precum masa, volumul, presiunea, temperatura și densitatea, care pot fi descrise printr-un număr obișnuit și sunt numite " scalari".
Ele sunt scrise fie cu litere de font obișnuit, fie cu cifre (a, b, t, G, 5, −7....). Mărimile scalare pot fi pozitive sau negative. În același timp, unele obiecte de studiu pot avea astfel de proprietăți care descriere completa Pentru care cunoașterea doar a unei măsuri numerice se dovedește a fi insuficientă, este necesară și caracterizarea acestor proprietăți prin direcția în spațiu. Astfel de proprietăți sunt caracterizate de mărimi vectoriale (vectori). Vectorii, spre deosebire de scalari, sunt notați cu litere aldine: a, b, g, F, C....
Adesea, un vector este notat printr-o literă cu font obișnuit (nebold), dar cu o săgeată deasupra:
În plus, un vector este adesea notat cu o pereche de litere (de obicei cu majuscule), prima literă indicând începutul vectorului, iar a doua sfârșitul acestuia.
Modulul unui vector, adică lungimea unui segment de linie dreaptă direcționată, este notat cu aceleași litere ca și vectorul însuși, dar în scris normal (nu îngroșat) și fără săgeată deasupra lor, sau exact în același mod ca vector (adică îngroșat sau regulat, dar cu săgeată), dar apoi desemnarea vectorului este închisă în liniuțe verticale.
Un vector este un obiect complex care este caracterizat simultan atât de mărime, cât și de direcție.
De asemenea, nu există vectori pozitivi și negativi. Dar vectorii pot fi egali între ei. Acesta este atunci când, de exemplu, a și b au aceleași module și sunt direcționate în aceeași direcție. În acest caz, notația este adevărată A= b. De asemenea, trebuie avut în vedere că simbolul vectorial poate fi precedat de un semn minus, de exemplu - c, cu toate acestea, acest semn indică simbolic că vectorul -c are același modul ca vectorul c, dar este direcționat în sens opus direcţie.
Vectorul -c se numește opusul (sau inversul) vectorului c.
În fizică, fiecare vector este umplut cu conținut specific, iar atunci când se compară vectori de același tip (de exemplu, forțe), punctele de aplicare a acestora pot fi, de asemenea, semnificative.
2. Determinarea proiecției, axei și coordonatei punctului.
Axă- Aceasta este o linie dreaptă căreia i se dă o anumită direcție.
O axă este desemnată printr-o literă: X, Y, Z, s, t... De obicei, pe axă este selectat (arbitrar) un punct, care se numește origine și, de regulă, este desemnat cu litera O. Din acest punct se măsoară distanțele până la alte puncte de interes pentru noi.
Proiecția unui punct pe o axă se află baza unei perpendiculare trasate din acest punct pe o axă dată. Adică proiecția unui punct pe axă este un punct.
Coordonata punctului pe o axă dată este un număr a cărui valoare absolută este egală cu lungimea segmentului de axă (pe scara selectată) cuprins între originea axei și proiecția punctului pe această axă. Acest număr se ia cu semnul plus dacă proiecția punctului este situată în direcția axei de la origine și cu semnul minus dacă este în sens opus.
3. Proiecția vectorului pe axă.
Proiecția unui vector pe o axă este un vector care se obține prin înmulțirea proiecției scalare a unui vector pe această axă și vectorul unitar al acestei axe. De exemplu, dacă a x este proiecția scalară a vectorului a pe axa X, atunci a x ·i este proiecția sa vectorială pe această axă.
Să notăm proiecția vectorială în același mod ca vectorul însuși, dar cu indicele axei pe care este proiectat vectorul. Astfel, notăm proiecția vectorială a vectorului a pe axa X ca x (litera îngroșată care indică vectorul și indicele numelui axei) sau
(o literă cu caractere aldine mici care denotă un vector, dar cu o săgeată în partea de sus (!) și un indice pentru numele axei).Proiecție scalară se numește vector pe axă număr, a cărui valoare absolută este egală cu lungimea segmentului de axă (pe scara selectată) cuprinsă între proiecțiile punctului de început și punctul final al vectorului. De obicei, în locul expresiei proiecție scalară pur și simplu spun - proiecție. Proiecția se notează cu aceeași literă cu vectorul proiectat (în scriere normală, fără caractere aldine), cu un indice mai mic (de regulă) al numelui axei pe care este proiectat acest vector. De exemplu, dacă un vector este proiectat pe axa X A, atunci proiecția sa se notează cu x. La proiectarea aceluiași vector pe o altă axă, dacă axa este Y, proiecția sa va fi notată cu y.
Pentru a calcula proiecția vector pe o axă (de exemplu, axa X), este necesar să se scadă coordonatele punctului de plecare din coordonatele punctului său final, adică
a x = x k − x n.
Proiecția unui vector pe o axă este un număr.În plus, proiecția poate fi pozitivă dacă valoarea x k este mai mare decât valoarea x n,
negativ dacă valoarea x k este mai mică decât valoarea x n
și egal cu zero dacă x k este egal cu x n.
Proiecția unui vector pe o axă poate fi găsită și cunoscând modulul vectorului și unghiul pe care îl formează cu această axă.
Din figură este clar că a x = a Cos α
Adică, proiecția vectorului pe axă este egală cu produsul dintre modulul vectorului și cosinusul unghiului dintre direcția axei și direcția vectorială. Dacă unghiul este ascuțit, atunci
Cos α > 0 și a x > 0 și, dacă este obtuz, atunci cosinusul unghiului obtuz este negativ, iar proiecția vectorului pe axă va fi, de asemenea, negativă.
Unghiurile măsurate de pe axa în sens invers acelor de ceasornic sunt considerate pozitive, iar unghiurile măsurate de-a lungul axei sunt negative. Totuși, deoarece cosinusul este o funcție pară, adică Cos α = Cos (− α), atunci când se calculează proiecțiile, unghiurile pot fi numărate atât în sensul acelor de ceasornic, cât și în sens invers acelor de ceasornic.
Pentru a găsi proiecția unui vector pe o axă, modulul acestui vector trebuie înmulțit cu cosinusul unghiului dintre direcția axei și direcția vectorului.
4. Formula de bază a algebrei vectoriale.
Să proiectăm vectorul a pe axele X și Y ale sistemului de coordonate dreptunghiulare. Să găsim proiecțiile vectoriale ale vectorului a pe aceste axe:
a x = a x ·i și y = a y ·j.
Dar în conformitate cu regula adunării vectoriale
a = a x + a y.
a = a x i + a y j.
Astfel, am exprimat un vector în termenii proiecțiilor sale și ai vectorilor sistemului de coordonate dreptunghiulare (sau în termenii proiecțiilor sale vectoriale).
Proiecțiile vectoriale a x și a y se numesc componente sau componente ale vectorului a. Operația pe care am efectuat-o se numește descompunerea unui vector de-a lungul axelor unui sistem de coordonate dreptunghiulare.
Dacă vectorul este dat în spațiu, atunci
a = a x i + a y j + a z k.
Această formulă se numește formula de bază a algebrei vectoriale. Desigur, se poate scrie așa.
Fie dată axa l în spațiu, adică o dreaptă direcționată.
Proiecția punctului M pe axa l este baza M 1 a perpendicularei MM 1 coborâtă din punct spre axă.
Punctul M 1 este punctul de intersecție al axei l cu un plan care trece prin punctul M perpendicular pe axă (vezi Fig. 7).
Dacă punctul M se află pe axa l, atunci proiecția punctului M pe axă coincide cu M1.
Fie AB un vector arbitrar (AB¹ 0). Să notăm cu A 1 și b 1 proiecțiile pe axa l, respectiv, a începutului A și a sfârșitului B a vectorului AB și să considerăm vectorul A 1 B 1
Proiecția vectorului AB pe axa l este numărul pozitiv |A 1 B 1 | , dacă vectorul A 1 B 1 și axa l sunt egal direcționate și numărul negativ este |A 1 B 1 | , dacă vectorul A 1 B 1 și axa l sunt direcționate opus (vezi Fig. 8). Dacă punctele a 1 și b 1 coincid (A 1 B 1 = 0), atunci proiecția vectorului AB este egală cu 0.
Proiecția vectorului AB pe axa l se notează astfel: pr l AB. Dacă AB=0 sau AB^l, atunci pr l AB=0.
Unghiul j dintre vectorul a și axa l (sau unghiul dintre doi vectori) este prezentat în figura 9. Evident, 0£j£p
Să ne uităm la câteva proprietăți de bază ale proiecțiilor.
Proprietatea 1. Proiecția vectorului a pe axa l este egală cu produsul dintre modulul vectorului a și cosinusul unghiului j dintre vector și axă, adică pr l a =|a | cos j .
Corolarul 5.1. Proiecția unui vector pe o axă este pozitivă (negativă) dacă vectorul formează un unghi ascuțit (obtuz) cu axa și este egală cu zero dacă acest unghi este drept.
Corolarul 5.2. Proiecțiile vectorilor egali pe aceeași axă sunt egale între ele.
Proprietatea 2. Proiecția sumei mai multor vectori pe aceeași axă este egală cu suma proiecțiilor lor pe această axă
Proprietatea 3. Când un vector a este înmulțit cu un număr A, proiecția lui pe axă se înmulțește și cu acest număr, adică.
Astfel, operațiile liniare pe vectori conduc la operații liniare corespunzătoare asupra proiecțiilor acestor vectori.
5.4. Descompunerea unui vector în vectori unitari ai axelor de coordonate.
Modul vectorial. Cosinusuri de direcție.
Să considerăm un sistem de coordonate dreptunghiular Oxyz în spațiu. Să selectăm vectori unitari (orturi) pe axele de coordonate Ox, Oy și Oz, notate i, j, k, respectiv (vezi Fig. 12).
Să alegem un vector arbitrar a de spațiu și să aliniem originea acestuia cu originea coordonatelor: a = OM.
Să găsim proiecțiile vectorului a pe axele de coordonate. Să desenăm plane paralele cu planurile de coordonate până la sfârșitul vectorului OM. Notăm punctele de intersecție ale acestor plane cu axele prin M 1, M 2 și respectiv M3 Obținem un paralelipiped dreptunghiular, una din diagonalele căruia este vectorul OM. Atunci pr x a=|OM 1 |, np y a = |OM 2 |, pr z a=|OM3|. Prin definirea sumei mai multor vectori, găsim a = OM 1 + M 1 N + NM.
Și întrucât M 1 N=OM 2, NM = OM3, atunci
a=OM 1 + OM 2 + OM 3 (5.1)
Să notăm proiecțiile vectorului a=OM pe axele Ox, Oy și, respectiv, Oz cu a x, a y și a z, i.e. |OM 1 | = a x,|OM 2 | = a y, |OM 3 | = a z . Apoi din egalitățile (5.1) și (5.2) obținem
a=a x i+a y j+a z k (5.3)
Această formulă este de bază în calculul vectorial și se numește descompunerea unui vector în vectori unitari ai axelor de coordonate. Numerele a x, a y, a z se numesc coordonatele vectorului a, adică coordonatele vectorului sunt proiecțiile acestuia pe axele de coordonate corespunzătoare.
Egalitatea vectorială (5.3) este adesea scrisă sub formă simbolică: a = (a x ;a y ;a z).
Egalitatea b = (b x; b y; b z) înseamnă că b = b x i + b y j + b z k. Cunoscând proiecțiile vectorului a, puteți găsi cu ușurință o expresie pentru modulul vectorului. Pe baza teoremei privind lungimea diagonalei unui paralelipiped dreptunghic, putem scrie
adică, modulul unui vector este egal cu rădăcina pătrată a sumei pătratelor proiecțiilor sale pe axele de coordonate.
Fie unghiurile vectorului a cu axele Ox, Oy și Oz egale cu a, b, g, respectiv. Prin proprietatea proiecției vectoriale pe axă, avem
Sau, ce este la fel,
Numerele se numesc cosinus de direcție ale vectorului a.
Înlocuind expresiile (5.5) în egalitatea (5.4), obținem
Reducând prin obținem relația
adică suma pătratelor cosinusurilor direcției unui vector diferit de zero este egală cu unu.
Este ușor de observat că coordonatele vectorului unitar e sunt numerele
Deci, specificând coordonatele unui vector, puteți determina oricând mărimea și direcția acestuia, adică. vectorul în sine.
Proiecția algebrică a unui vector pe orice axă este egal cu produsul dintre lungimea vectorului și cosinusul unghiului dintre axă și vector:Pr a b = |b|cos(a,b) sau
Unde a b este produsul scalar al vectorilor, |a| - modulul vectorului a.
Instrucțiuni. Pentru a găsi proiecția vectorului Pr a b online, trebuie să specificați coordonatele vectorilor a și b. În acest caz, vectorul poate fi specificat în plan (două coordonate) și în spațiu (trei coordonate). Soluția rezultată este salvată într-un fișier Word. Dacă vectorii sunt specificați prin coordonatele punctelor, atunci trebuie să utilizați acest calculator.
Clasificarea proiecțiilor vectoriale
Tipuri de proiectii prin definitie proiectie vectoriala
- Proiecția geometrică a vectorului AB pe axă (vector) se numește vector A"B", începutul căruia A' este proiecția începutului A pe axă (vector), iar capătul B' este proiecția capătului B pe aceeași axă.
- Proiecția algebrică a vectorului AB pe axă (vector) se numește lungimea vectorului A"B", luată cu semnul + sau -, în funcție de faptul că vectorul A"B" are aceeași direcție ca axa ( vector).
Tipuri de proiecții în funcție de sistemul de coordonate
Proprietăți de proiecție vectorială
- Proiecția geometrică a unui vector este un vector (are o direcție).
- Proiecția algebrică a unui vector este un număr.
Teoreme de proiecție vectorială
Teorema 1. Proiecția sumei vectorilor pe orice axă este egală cu proiecția sumelor vectorilor pe aceeași axă.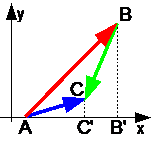 AC" =AB" +B"C"
AC" =AB" +B"C"
Teorema 2. Proiecția algebrică a unui vector pe orice axă este egală cu produsul dintre lungimea vectorului și cosinusul unghiului dintre axă și vector:
Pr a b = |b|·cos(a,b)
Tipuri de proiectii vectoriale
- proiecție pe axa OX.
- proiecție pe axa OY.
- proiecție pe un vector.
| Proiecție pe axa OX | Proiecție pe axa OY | Proiecție la vector |
Dacă direcția vectorului A’B’ coincide cu direcția axei OX, atunci proiecția vectorului A’B’ are semn pozitiv.  | Dacă direcția vectorului A’B’ coincide cu direcția axei OY, atunci proiecția vectorului A’B’ are semn pozitiv.  | Dacă direcția vectorului A’B’ coincide cu direcția vectorului NM, atunci proiecția vectorului A’B’ are semn pozitiv.  |
Dacă direcția vectorului este opusă direcției axei OX, atunci proiecția vectorului A’B’ are semn negativ.
 | Dacă direcția vectorului A’B’ este opusă direcției axei OY, atunci proiecția vectorului A’B’ are semn negativ. | Dacă direcția vectorului A’B’ este opusă direcției vectorului NM, atunci proiecția vectorului A’B’ are semn negativ.  |
Dacă vectorul AB este paralel cu axa OX, atunci proiecția vectorului A’B’ este egală cu valoarea absolută a vectorului AB.   | Dacă vectorul AB este paralel cu axa OY, atunci proiecția vectorului A’B’ este egală cu valoarea absolută a vectorului AB.   | Dacă vectorul AB este paralel cu vectorul NM, atunci proiecția vectorului A’B’ este egală cu valoarea absolută a vectorului AB.   |
Dacă vectorul AB este perpendicular pe axa OX, atunci proiecția A’B’ este egală cu zero (vector nul).   | Dacă vectorul AB este perpendicular pe axa OY, atunci proiecția A’B’ este egală cu zero (vector nul).   | Dacă vectorul AB este perpendicular pe vectorul NM, atunci proiecția A’B’ este egală cu zero (vector nul).   |
1. Întrebare: Proiectia unui vector poate avea semn negativ? Răspuns: Da, vectorul de proiecție poate fi o valoare negativă. În acest caz, vectorul are direcția opusă (vezi cum sunt direcționate axa OX și vectorul AB)
2. Întrebare: Poate să coincidă proiecția unui vector cu valoarea absolută a vectorului? Răspuns: Da, se poate. În acest caz, vectorii sunt paraleli (sau se află pe aceeași linie).
3. Întrebare: Poate fi proiecția unui vector egală cu zero (vector nul). Răspuns: Da, se poate. În acest caz, vectorul este perpendicular pe axa corespunzătoare (vector).
Exemplul 1. Vectorul (Fig. 1) formează un unghi de 60° cu axa OX (este specificat de vectorul a). Dacă OE este o unitate de scară, atunci |b|=4, deci ![]() .
.

Într-adevăr, lungimea vectorului (proiecția geometrică b) este egală cu 2, iar direcția coincide cu direcția axei OX.
Exemplul 2. Vectorul (Fig. 2) formează un unghi (a,b) = 120 o cu axa OX (cu vectorul a). Lungimea |b| vectorul b este egal cu 4, deci pr a b=4·cos120 o = -2. 
Într-adevăr, lungimea vectorului este 2, iar direcția este opusă direcției axei.