Πώς να βρείτε την προβολή ενός διανύσματος στους άξονες συντεταγμένων. Διανύσματα και πράξεις σε διανύσματα. Διανυσματικές ιδιότητες προβολής

17.09.2021Επικεφαλίδα: Είδη

Ορισμός 1. Σε ένα επίπεδο, η παράλληλη προβολή του σημείου Α στον άξονα l είναι ένα σημείο - το σημείο τομής του άξονα l με μια ευθεία γραμμή που διασχίζεται από το σημείο Α παράλληλη προς το διάνυσμα που καθορίζει την κατεύθυνση σχεδιασμού.

Ορισμός 2. Η παράλληλη προβολή ενός διανύσματος στον άξονα l (σε ένα διάνυσμα) είναι η συντεταγμένη του διανύσματος, σε σχέση με τη βάση τον άξονα l, όπου τα σημεία και είναι παράλληλες προεξοχές των σημείων Α και Β, αντίστοιχα, στον άξονα l (Εικ. 1).

Εξ ορισμού, έχουμε

Ορισμός 3. αν και τη βάση του άξονα l καρτεσιανή, δηλαδή, τότε η προβολή του διανύσματος στον άξονα l ονομάζεται ορθογώνιο (Εικ. 2).

Στο χώρο, ο ορισμός 2 της προβολής ενός διανύσματος σε έναν άξονα παραμένει έγκυρος, μόνο η κατεύθυνση προβολής δίνεται από δύο μη συγγραμμικά διανύσματα (Εικ. 3).

Από τον ορισμό της προβολής ενός διανύσματος σε έναν άξονα, προκύπτει ότι κάθε συντεταγμένη του διανύσματος είναι η προβολή αυτού του διανύσματος στον άξονα που καθορίζεται από το αντίστοιχο διάνυσμα βάσης. Σε αυτή την περίπτωση, η κατεύθυνση σχεδιασμού ορίζεται από δύο άλλα διανύσματα βάσης, εάν η σχεδίαση εκτελείται (εξετάζεται) στο χώρο, ή από άλλο διάνυσμα βάσης, εάν η σχεδίαση εξετάζεται σε επίπεδο (Εικ. 4).

Θεώρημα 1. Η ορθογώνια προβολή ενός διανύσματος στον άξονα l είναι ίση με το γινόμενο του συντελεστή του διανύσματος και του συνημιτόνου της γωνίας μεταξύ της θετικής κατεύθυνσης του άξονα l και, δηλ.

Στην άλλη πλευρά

Από βρίσκουμε

Αντικαθιστώντας το AC με την ισότητα (2), λαμβάνουμε

Από τους αριθμούς Χκαι του ίδιου σημείου και στις δύο εξεταζόμενες περιπτώσεις ((Εικ. 5, α) ; (Σχ. 5, β) , τότε η ισότητα (4) συνεπάγεται

Σχόλιο. Στο μέλλον, θα εξετάσουμε μόνο την ορθογώνια προβολή του διανύσματος στον άξονα και επομένως η λέξη "orth" (ορθογώνιο) στη σημειογραφία θα παραλειφθεί.

Παρουσιάζουμε έναν αριθμό τύπων που χρησιμοποιούνται στο μέλλον κατά την επίλυση προβλημάτων.

α) Προβολή ενός διανύσματος σε έναν άξονα.

Αν, τότε η ορθογώνια προβολή πάνω στο διάνυσμα σύμφωνα με τον τύπο (5) έχει τη μορφή

γ) Απόσταση από σημείο σε επίπεδο.

Έστω b ένα δεδομένο επίπεδο με κανονικό διάνυσμα, M ένα δεδομένο σημείο,

d - απόσταση από το σημείο M στο επίπεδο b (Εικ. 6).

Αν το N είναι ένα αυθαίρετο σημείο του επιπέδου b και είναι οι προβολές των σημείων M και N στον άξονα, τότε

ΣΟΛ) Απόσταση μεταξύ τεμνόμενων γραμμών.

Έστω στις α και β τεμνόμενες ευθείες, ένα διάνυσμα κάθετο σε αυτές, το Α και Β είναι αυθαίρετα σημεία των ευθειών a και b, αντίστοιχα (Εικ. 7) και προβολές των σημείων Α και Β επάνω, τότε

ε) Απόσταση από σημείο σε ευθεία.

Αφήνω μεγάλο- δεδομένη ευθεία με διάνυσμα κατεύθυνσης, M - δεδομένο σημείο,

N - η προβολή του στη γραμμή μεγάλο, στη συνέχεια - την επιθυμητή απόσταση (Εικ. 8).

Αν το Α είναι ένα αυθαίρετο σημείο της ευθείας μεγάλο, τότε στο ορθογώνιο τρίγωνο MNA μπορεί να βρεθεί η υποτείνουσα ΜΑ και τα σκέλη. Που σημαίνει,

ε) Γωνία μεταξύ ευθείας και επιπέδου.

Έστω το διάνυσμα κατεύθυνσης της δεδομένης ευθείας μεγάλο, - κανονικό διάνυσμα του δεδομένου επιπέδου b, - προβολή ευθείας γραμμής μεγάλοστο επίπεδο b (Εικ. 9).

Όπως γνωρίζετε, η γωνία q μεταξύ της ευθείας μεγάλοκαι η προβολή του στο επίπεδο b ονομάζεται γωνία μεταξύ της ευθείας και του επιπέδου. Εχουμε

Ας δώσουμε παραδείγματα επίλυσης μετρικών προβλημάτων με τη μέθοδο διανύσματος-συντεταγμένων.

Αρχικά, ας θυμηθούμε τι είναι άξονα συντεταγμένων, προβολή ενός σημείου σε έναν άξονακαι συντεταγμένες ενός σημείου στον άξονα.

Άξονας συντεταγμένωνείναι μια ευθεία που της δίνεται κατεύθυνση. Μπορείτε να το σκεφτείτε ως ένα διάνυσμα με απείρως μεγάλο συντελεστή.

Άξονας συντεταγμένωνσυμβολίζεται με οποιοδήποτε γράμμα: X, Y, Z, s, t ... Συνήθως, επιλέγεται ένα σημείο (αυθαίρετα) στον άξονα, το οποίο ονομάζεται αρχή και, κατά κανόνα, συμβολίζεται με το γράμμα O. Αποστάσεις από άλλα Τα σημεία που μας ενδιαφέρουν μετρώνται από αυτό το σημείο.

Προβολή σημείου πάνω σε άξονα- αυτή είναι η βάση της καθέτου που έπεσε από αυτό το σημείο στον δεδομένο άξονα (Εικ. 8). Δηλαδή, η προβολή ενός σημείου πάνω στον άξονα είναι ένα σημείο.

Σημειακή συντεταγμένη ανά άξοναείναι ο αριθμός απόλυτη τιμήπου είναι ίσο με το μήκος του τμήματος του άξονα (στην επιλεγμένη κλίμακα) που περικλείεται μεταξύ της αρχής του άξονα και της προβολής του σημείου στον άξονα αυτόν. Ο αριθμός αυτός λαμβάνεται με πρόσημο συν αν η προβολή του σημείου βρίσκεται στην κατεύθυνση του άξονα από την αρχή του και με αρνητικό αν βρίσκεται στην αντίθετη κατεύθυνση.

Κλιμακωτή προβολή ενός διανύσματος σε έναν άξονα- αυτό αριθμός, η απόλυτη τιμή του οποίου ισούται με το μήκος του τμήματος του άξονα (στην επιλεγμένη κλίμακα) που περικλείεται μεταξύ των προβολών του σημείου έναρξης και του σημείου τέλους του διανύσματος. Σπουδαίος! Συνήθως αντί της έκφρασης κλιμακωτή προβολή ενός διανύσματος σε έναν άξονααπλά λένε - προβολή ενός διανύσματος σε έναν άξονα, δηλαδή η λέξη βαθμωτό μέγεθοςχαμηλωμένο. Διάνυσμα προβολήςσυμβολίζεται με το ίδιο γράμμα με το προβαλλόμενο διάνυσμα (σε κανονική, μη έντονη γραφή), με δείκτη (συνήθως) του ονόματος του άξονα στον οποίο προβάλλεται αυτό το διάνυσμα. Για παράδειγμα, εάν ένα διάνυσμα προβάλλεται στον άξονα x ένα,τότε η προβολή του συμβολίζεται με x . Όταν προβάλλετε το ίδιο διάνυσμα σε έναν άλλο άξονα, ας πούμε τον άξονα Y, η προβολή του θα συμβολίζεται ως y (Εικ. 9).

Να υπολογίσω διανυσματική προβολή στον άξονα(για παράδειγμα, ο άξονας Χ) είναι απαραίτητο να αφαιρέσετε τη συντεταγμένη του σημείου έναρξης από τη συντεταγμένη του τελικού σημείου του, δηλαδή

και x \u003d x k - x n.

Πρέπει να θυμόμαστε: η κλιμακωτή προβολή ενός διανύσματος σε έναν άξονα (ή, απλά, η προβολή ενός διανύσματος σε έναν άξονα) είναι αριθμός (όχι διάνυσμα)!Επιπλέον, η προβολή μπορεί να είναι θετική εάν η τιμή x k είναι μεγαλύτερη από την τιμή x n, αρνητική εάν η τιμή x k είναι μικρότερη από την τιμή x n και ίση με μηδέν εάν το x k είναι ίση με x n (Εικ. 10).

Η προβολή ενός διανύσματος σε έναν άξονα μπορεί επίσης να βρεθεί γνωρίζοντας το μέτρο του διανύσματος και τη γωνία που κάνει με αυτόν τον άξονα.

Το σχήμα 11 δείχνει ότι a x = a Cos α

Δηλαδή, η προβολή του διανύσματος στον άξονα είναι ίση με το γινόμενο του διανυσματικού μέτρου και του συνημιτόνου της γωνίας μεταξύ κατεύθυνσης άξονα και διεύθυνσης διανύσματος. Εάν η γωνία είναι οξεία, τότε Cos α > 0 και a x > 0, και αν είναι αμβλεία, τότε το συνημίτονο της αμβλείας γωνίας είναι αρνητικό και η προβολή του διανύσματος στον άξονα θα είναι επίσης αρνητική.

Οι γωνίες που μετρώνται από τον άξονα αριστερόστροφα θεωρούνται θετικές και προς την κατεύθυνση αρνητικές. Ωστόσο, δεδομένου ότι το συνημίτονο είναι άρτια συνάρτηση, δηλαδή Cos α = Cos (− α), τότε κατά τον υπολογισμό των προβολών, οι γωνίες μπορούν να μετρηθούν τόσο δεξιόστροφα όσο και αριστερόστροφα.

Κατά την επίλυση προβλημάτων, συχνά χρησιμοποιούνται οι ακόλουθες ιδιότητες των προβολών: αν

ένα = σι + ντο +…+ ρε, τότε a x = b x + c x +…+ d x (ομοίως για άλλους άξονες),

ένα= m σι, τότε a x = mb x (ομοίως για άλλους άξονες).

Ο τύπος a x = a Cos α θα είναι Συχνάσυναντιούνται κατά την επίλυση προβλημάτων, επομένως πρέπει να είναι γνωστό. Πρέπει να γνωρίζετε τον κανόνα για τον προσδιορισμό της προβολής απεξω!

Θυμάμαι!

Για να βρεθεί η προβολή ενός διανύσματος σε έναν άξονα, το δομοστοιχείο αυτού του διανύσματος πρέπει να πολλαπλασιαστεί με το συνημίτονο της γωνίας μεταξύ της διεύθυνσης του άξονα και της διεύθυνσης του διανύσματος.

Για άλλη μια φορά - ΓΡΗΓΟΡΑ!

Εισαγωγή…………………………………………………………………………………… 3

1. Η τιμή ενός διανύσματος και ενός κλιμακωτή………………………………………………….4

2. Ορισμός προβολής, άξονα και συντεταγμένων σημείου……………………5

3. Διάνυσμα προβολή στον άξονα………………………………………………………………………

4. Ο βασικός τύπος της διανυσματικής άλγεβρας……………………………..8

5. Υπολογισμός της ενότητας του διανύσματος από τις προβολές του……………………9

Συμπέρασμα…………………………………………………………………………………….

Λογοτεχνία……………………………………………………………………………….12

Εισαγωγή:

Η φυσική είναι άρρηκτα συνδεδεμένη με τα μαθηματικά. Τα μαθηματικά δίνουν στη φυσική τα μέσα και τις τεχνικές μιας γενικής και ακριβούς έκφρασης της σχέσης μεταξύ φυσικών μεγεθών που ανακαλύπτονται ως αποτέλεσμα πειράματος ή θεωρητικής έρευνας.Τελικά, η κύρια μέθοδος έρευνας στη φυσική είναι η πειραματική. Αυτό σημαίνει ότι ο επιστήμονας αποκαλύπτει τους υπολογισμούς με τη βοήθεια μετρήσεων. Δηλώνει τη σχέση μεταξύ διαφορετικών φυσικών μεγεθών. Στη συνέχεια, όλα μεταφράζονται στη γλώσσα των μαθηματικών. Σχηματίστηκε μαθηματικό μοντέλο. Η φυσική είναι μια επιστήμη που μελετά τους απλούστερους και ταυτόχρονα τους πιο γενικούς νόμους. Το καθήκον της φυσικής είναι να δημιουργήσει στο μυαλό μας μια τέτοια εικόνα του φυσικού κόσμου που να αντικατοπτρίζει πλήρως τις ιδιότητές του και να παρέχει τέτοιες σχέσεις μεταξύ των στοιχείων του μοντέλου που υπάρχουν μεταξύ των στοιχείων.

Έτσι, η φυσική δημιουργεί ένα μοντέλο του κόσμου γύρω μας και μελετά τις ιδιότητές του. Αλλά οποιοδήποτε μοντέλο είναι περιορισμένο. Κατά τη δημιουργία μοντέλων ενός συγκεκριμένου φαινομένου, λαμβάνονται υπόψη μόνο ιδιότητες και συνδέσεις που είναι απαραίτητες για ένα δεδομένο φάσμα φαινομένων. Αυτή είναι η τέχνη ενός επιστήμονα - από όλη την ποικιλία να επιλέξει το κύριο πράγμα.

Τα φυσικά μοντέλα είναι μαθηματικά, αλλά τα μαθηματικά δεν είναι η βάση τους. Οι ποσοτικές σχέσεις μεταξύ φυσικών μεγεθών διευκρινίζονται ως αποτέλεσμα μετρήσεων, παρατηρήσεων και πειραματικών μελετών και εκφράζονται μόνο στη γλώσσα των μαθηματικών. Ωστόσο, δεν υπάρχει άλλη γλώσσα για την κατασκευή φυσικών θεωριών.

1. Η τιμή ενός διανύσματος και ενός κλιμακωτή.

Στη φυσική και στα μαθηματικά, διάνυσμα είναι ένα μέγεθος που χαρακτηρίζεται από την αριθμητική του τιμή και την κατεύθυνση. Στη φυσική, υπάρχουν πολλά σημαντικά μεγέθη που είναι διανύσματα, όπως δύναμη, θέση, ταχύτητα, επιτάχυνση, ροπή, ορμή, ηλεκτρικά και μαγνητικά πεδία. Μπορούν να αντιπαραβληθούν με άλλες ποσότητες, όπως μάζα, όγκος, πίεση, θερμοκρασία και πυκνότητα, που μπορούν να περιγραφούν με έναν συνηθισμένο αριθμό, και ονομάζονται " σκαλοπάτια".

Γράφονται είτε με γράμματα κανονικής γραμματοσειράς, είτε με αριθμούς (a, b, t, G, 5, -7 ....). Οι βαθμίδες μπορεί να είναι θετικές ή αρνητικές. Ταυτόχρονα, ορισμένα αντικείμενα μελέτης μπορεί να έχουν τέτοιες ιδιότητες, για μια πλήρη περιγραφή των οποίων η γνώση μόνο ενός αριθμητικού μέτρου είναι ανεπαρκής, είναι επίσης απαραίτητο να χαρακτηριστούν αυτές οι ιδιότητες από μια κατεύθυνση στο χώρο. Τέτοιες ιδιότητες χαρακτηρίζονται από διανυσματικές ποσότητες (διανύσματα). Τα διανύσματα, σε αντίθεση με τους βαθμωτούς, σημειώνονται με έντονα γράμματα: a, b, g, F, C ....
Συχνά, ένα διάνυσμα συμβολίζεται με ένα κανονικό (μη έντονο) γράμμα, αλλά με ένα βέλος πάνω από αυτό:

Επιπλέον, ένα διάνυσμα συχνά υποδηλώνεται με ένα ζεύγος γραμμάτων (συνήθως με κεφαλαία γράμματα), με το πρώτο γράμμα να δείχνει την αρχή του διανύσματος και το δεύτερο γράμμα να δείχνει το τέλος του.

Το δομοστοιχείο του διανύσματος, δηλαδή το μήκος του κατευθυνόμενου ευθύγραμμου τμήματος, συμβολίζεται με τα ίδια γράμματα με το ίδιο το διάνυσμα, αλλά με τη συνήθη (μη έντονη) γραφή και χωρίς βέλος από πάνω τους ή ακριβώς όπως το διάνυσμα (δηλαδή με έντονη γραφή ή κανονικό, αλλά με βέλος), αλλά στη συνέχεια ο προσδιορισμός του διανύσματος περικλείεται σε κάθετες παύλες.
Ένα διάνυσμα είναι ένα σύνθετο αντικείμενο που χαρακτηρίζεται από το μέγεθος και την κατεύθυνση ταυτόχρονα.

Επίσης δεν υπάρχουν θετικά και αρνητικά διανύσματα. Αλλά τα διανύσματα μπορεί να είναι ίσα μεταξύ τους. Αυτό συμβαίνει όταν, για παράδειγμα, τα a και b έχουν τις ίδιες μονάδες και κατευθύνονται προς την ίδια κατεύθυνση. Σε αυτή την περίπτωση, το ρεκόρ ένα= β. Θα πρέπει επίσης να ληφθεί υπόψη ότι το σύμβολο του διανύσματος μπορεί να προηγείται από ένα σύμβολο μείον, για παράδειγμα, -c, ωστόσο, αυτό το σύμβολο υποδηλώνει συμβολικά ότι το διάνυσμα -c έχει τον ίδιο συντελεστή με το διάνυσμα c, αλλά κατευθύνεται στο αντίθετη κατεύθυνση.

Το διάνυσμα -c ονομάζεται αντίθετο (ή αντίστροφο) του διανύσματος c.
Στη φυσική, ωστόσο, κάθε διάνυσμα είναι γεμάτο με συγκεκριμένο περιεχόμενο και κατά τη σύγκριση διανυσμάτων του ίδιου τύπου (για παράδειγμα, δυνάμεις), τα σημεία εφαρμογής τους μπορεί επίσης να έχουν σημαντική σημασία.

2.Προσδιορισμός της προβολής, του άξονα και της συντεταγμένης του σημείου.

Αξοναςείναι μια ευθεία που της δίνεται κατεύθυνση.
Ο άξονας υποδεικνύεται με οποιοδήποτε γράμμα: X, Y, Z, s, t ... Συνήθως, επιλέγεται (αυθαίρετα) ένα σημείο στον άξονα, το οποίο ονομάζεται αρχή και, κατά κανόνα, δηλώνεται με το γράμμα Ο Από αυτό το σημείο μετρώνται οι αποστάσεις από άλλα σημεία ενδιαφέροντος για εμάς.

σημειακή προβολήστον άξονα λέγεται η βάση της καθέτου που έπεσε από αυτό το σημείο στον δεδομένο άξονα. Δηλαδή, η προβολή ενός σημείου πάνω στον άξονα είναι ένα σημείο.

συντεταγμένη σημείουσε έναν δεδομένο άξονα ονομάζεται ένας αριθμός του οποίου η απόλυτη τιμή ισούται με το μήκος του τμήματος του άξονα (στην επιλεγμένη κλίμακα) που περικλείεται μεταξύ της αρχής του άξονα και της προβολής του σημείου σε αυτόν τον άξονα. Ο αριθμός αυτός λαμβάνεται με πρόσημο συν αν η προβολή του σημείου βρίσκεται στην κατεύθυνση του άξονα από την αρχή του και με αρνητικό αν βρίσκεται στην αντίθετη κατεύθυνση.

3.Προβολή ενός διανύσματος πάνω σε έναν άξονα.

Η προβολή ενός διανύσματος σε έναν άξονα είναι ένα διάνυσμα που προκύπτει πολλαπλασιάζοντας τη βαθμιδωτή προβολή ενός διανύσματος σε αυτόν τον άξονα και το μοναδιαίο διάνυσμα αυτού του άξονα. Για παράδειγμα, αν a x είναι η βαθμιδωτή προβολή του διανύσματος a στον άξονα Χ, τότε το x i είναι η διανυσματική προβολή του σε αυτόν τον άξονα.

Ας υποδηλώσουμε τη διανυσματική προβολή με τον ίδιο τρόπο όπως το ίδιο το διάνυσμα, αλλά με τον δείκτη του άξονα στον οποίο προβάλλεται το διάνυσμα. Έτσι, η διανυσματική προβολή του διανύσματος a στον άξονα Χ συμβολίζεται με ένα x (έντονο γράμμα που δηλώνει το διάνυσμα και τον δείκτη του ονόματος του άξονα) ή

(χωρίς έντονο γράμμα που δηλώνει διάνυσμα, αλλά με βέλος στην κορυφή (!) και δείκτη του ονόματος του άξονα).

Σκαλική προβολήδιάνυσμα ανά άξονα ονομάζεται αριθμός, η απόλυτη τιμή του οποίου ισούται με το μήκος του τμήματος του άξονα (στην επιλεγμένη κλίμακα) που περικλείεται μεταξύ των προβολών του σημείου έναρξης και του σημείου τέλους του διανύσματος. Συνήθως αντί της έκφρασης κλιμακωτή προβολήαπλά πες - προβολή. Η προβολή συμβολίζεται με το ίδιο γράμμα με το προβαλλόμενο διάνυσμα (σε κανονική, μη έντονη γραφή), με δείκτη (συνήθως) του ονόματος του άξονα στον οποίο προβάλλεται αυτό το διάνυσμα. Για παράδειγμα, εάν ένα διάνυσμα προβάλλεται στον άξονα x ένα,τότε η προβολή του συμβολίζεται με x . Όταν προβάλλεται το ίδιο διάνυσμα σε άλλο άξονα, εάν ο άξονας είναι Y , η προβολή του θα συμβολίζεται ως y .

Για τον υπολογισμό της προβολής διάνυσμασε έναν άξονα (για παράδειγμα, τον άξονα Χ) είναι απαραίτητο να αφαιρέσετε τη συντεταγμένη του σημείου έναρξης από τη συντεταγμένη του τελικού σημείου του, δηλαδή

και x \u003d x k - x n.

Η προβολή ενός διανύσματος σε έναν άξονα είναι ένας αριθμός.Επιπλέον, η προβολή μπορεί να είναι θετική εάν η τιμή του x k είναι μεγαλύτερη από την τιμή του x n,

αρνητικό αν η τιμή του x k είναι μικρότερη από την τιμή του x n

και ίσο με μηδέν αν το x k είναι ίσο με x n.

Από το σχήμα φαίνεται ότι a x = a Cos α

Δηλαδή, η προβολή του διανύσματος στον άξονα είναι ίση με το γινόμενο του συντελεστή του διανύσματος και του συνημιτόνου της γωνίας μεταξύ της διεύθυνσης του άξονα και του διανυσματική κατεύθυνση. Αν η γωνία είναι οξεία, τότε
Συν α > 0 και a x > 0, και αν είναι αμβλεία, τότε το συνημίτονο αμβλείας γωνίας είναι αρνητικό και η προβολή του διανύσματος στον άξονα θα είναι επίσης αρνητική.

Οι γωνίες που μετρώνται από τον άξονα αριστερόστροφα θεωρούνται θετικές και προς την κατεύθυνση αρνητικές. Ωστόσο, δεδομένου ότι το συνημίτονο είναι άρτια συνάρτηση, δηλαδή Cos α = Cos (− α), κατά τον υπολογισμό των προβολών, οι γωνίες μπορούν να μετρηθούν τόσο δεξιόστροφα όσο και αριστερόστροφα.

4. Βασικός τύπος διανυσματικής άλγεβρας.

Προβάλλουμε ένα διάνυσμα α στους άξονες Χ και Υ ενός ορθογώνιου συστήματος συντεταγμένων. Βρείτε τις διανυσματικές προβολές του διανύσματος a σε αυτούς τους άξονες:

και x = a x i, και y = a y j.

Αλλά σύμφωνα με τον κανόνα πρόσθεσης διανυσμάτων

a \u003d a x + a y.

a = a x i + a y j.

Έτσι, έχουμε εκφράσει ένα διάνυσμα ως προς τις προβολές του και τις στροφές ενός ορθογώνιου συστήματος συντεταγμένων (ή ως προς τις διανυσματικές προβολές του).

Οι διανυσματικές προβολές a x και a y ονομάζονται συνιστώσες ή συνιστώσες του διανύσματος α. Η πράξη που πραγματοποιήσαμε ονομάζεται αποσύνθεση του διανύσματος κατά μήκος των αξόνων ενός ορθογώνιου συστήματος συντεταγμένων.

Αν το διάνυσμα δίνεται στο χώρο, τότε

a = a x i + a y j + a z k.

Αυτός ο τύπος ονομάζεται βασικός τύπος της διανυσματικής άλγεβρας. Φυσικά, μπορεί να γραφτεί και έτσι.

Ας δοθεί ο άξονας l στο διάστημα, δηλ. μια κατευθυνόμενη ευθεία γραμμή.

Η προβολή του σημείου Μ στον άξονα l είναι η βάση Μ 1 της κάθετης ΜΜ 1, χαμηλωμένη από το σημείο προς τον άξονα.

Το σημείο M 1 είναι το σημείο τομής του άξονα l με ένα επίπεδο που διέρχεται από το σημείο M που είναι κάθετο στον άξονα (βλ. Εικ. 7).

Εάν το σημείο M βρίσκεται στον άξονα l, τότε η προβολή του σημείου M στον άξονα συμπίπτει με το M1.

Έστω AB ένα αυθαίρετο διάνυσμα (AB1 0). Ας συμβολίσουμε με A 1 και b 1 τις προβολές στον άξονα l, αντίστοιχα, της αρχής A και του τέλους B του διανύσματος AB και ας θεωρήσουμε το διάνυσμα A 1 B 1

Η προβολή του διανύσματος ΑΒ στον άξονα l είναι θετικός αριθμός |A 1 B 1 | , αν το διάνυσμα A 1 B 1 και ο άξονας l είναι ίσα κατευθυνόμενοι και αρνητικός αριθμός - |A 1 B 1 | , αν το διάνυσμα A 1 B 1 και ο άξονας l έχουν αντίθετη κατεύθυνση (βλ. Εικ. 8). Εάν τα σημεία a 1 και b 1 συμπίπτουν (A 1 B 1 \u003d 0), τότε η προβολή του διανύσματος AB είναι 0.

Η προβολή του διανύσματος ΑΒ στον άξονα l συμβολίζεται ως εξής: pr μεγάλοΑΒ. Αν AB=0 ή AB^l , τότε pr l AB=0.

Η γωνία j μεταξύ του διανύσματος a και του άξονα l (ή η γωνία μεταξύ δύο διανυσμάτων) φαίνεται στο σχήμα 9. Προφανώς, 0£j£p

Ας εξετάσουμε μερικές βασικές ιδιότητες των προβολών.

Ιδιότητα 1. Η προβολή του διανύσματος a στον άξονα l είναι ίση με το γινόμενο του συντελεστή του διανύσματος a και του συνημιτόνου της γωνίας j μεταξύ του διανύσματος και του άξονα, δηλ. pr l a =|a | cos j .

Συμπέρασμα 5.1. Η προβολή του διανύσματος στον άξονα είναι θετική (αρνητική) αν το διάνυσμα σχηματίζει οξεία (αμβλεία) γωνία με τον άξονα και είναι ίση με μηδέν αν αυτή η γωνία είναι ορθή.

Συμπέρασμα 5.2. Οι προβολές ίσων διανυσμάτων στον ίδιο άξονα είναι ίσες μεταξύ τους.

Ιδιότητα 2. Η προβολή του αθροίσματος πολλών διανυσμάτων στον ίδιο άξονα είναι ίση με το άθροισμα των προβολών τους σε αυτόν τον άξονα

Ιδιότητα 3. Όταν ένα διάνυσμα a πολλαπλασιάζεται με έναν αριθμό Α, η προβολή του στον άξονα πολλαπλασιάζεται επίσης με αυτόν τον αριθμό, δηλ.

Έτσι, οι γραμμικές πράξεις σε διανύσματα οδηγούν σε αντίστοιχες γραμμικές πράξεις στις προβολές αυτών των διανυσμάτων.

5.4. Αποσύνθεση ενός διανύσματος ως προς τα μοναδιαία διανύσματα των αξόνων συντεταγμένων.
Διάνυσμα ενότητα. Συνημίτονα κατεύθυνσης.

Θεωρήστε στο διάστημα ένα ορθογώνιο σύστημα συντεταγμένων Oxyz. Ξεχωρίζουμε μοναδιαία διανύσματα (orts) στους άξονες συντεταγμένων Ox, Oy και Oz, που συμβολίζονται με i, j, k, αντίστοιχα (βλ. Εικ. 12).

Επιλέγουμε ένα αυθαίρετο διάνυσμα α του χώρου και αντιστοιχίζουμε την αρχή του με την αρχή: a=OM.

Ας βρούμε τις προβολές του διανύσματος α στους άξονες συντεταγμένων. Ας σχεδιάσουμε το τέλος του διανύσματος ΟΜ επίπεδα παράλληλα με τα επίπεδα συντεταγμένων. Τα σημεία τομής αυτών των επιπέδων με τους άξονες θα συμβολίζονται αντίστοιχα με M 1 , M 2 και Mz. Παίρνουμε ένα ορθογώνιο παραλληλεπίπεδο, μία από τις διαγώνιες του οποίου είναι το διάνυσμα ΟΜ. Τότε pr x a=|OM 1 |, np y a = |OM 2 |, pr z a=|OM3|. Εξ ορισμού του αθροίσματος πολλών διανυσμάτων, βρίσκουμε a = OM 1 + M 1 N + NM.

Και αφού M 1 N \u003d OM 2, NM \u003d OM, τότε

a \u003d OM 1 + OM 2 + OM 3 (5.1)

Ας ορίσουμε τις προβολές του διανύσματος a=OM στους άξονες Ox, Oy και Oz, αντίστοιχα, ως x, a y και a z , δηλ. |ΟΜ 1 | = a x,|OM 2 | = a y, |OM 3 | = a z . Στη συνέχεια, από τις ισότητες (5.1) και (5.2) προκύπτει

a=a x i+a y j+a z k (5.3)

Αυτός ο τύπος είναι ο κύριος στον διανυσματικό λογισμό και ονομάζεται επέκταση ενός διανύσματος ως προς τα διανύσματα των αξόνων συντεταγμένων. Οι αριθμοί a x, a y, a z ονομάζονται συντεταγμένες του διανύσματος a, δηλαδή οι συντεταγμένες του διανύσματος είναι οι προβολές του στους αντίστοιχους άξονες συντεταγμένων.

Η διανυσματική ισότητα (5.3) συχνά γράφεται με συμβολική μορφή: a = (a x ;a y ;a z).

Η ισότητα b \u003d (b x; b y; b z) σημαίνει ότι b \u003d b x i + b y j + b z k. Γνωρίζοντας τις προβολές του διανύσματος α, μπορεί κανείς εύκολα να βρει μια έκφραση για το μέτρο του διανύσματος. Με βάση το θεώρημα για το μήκος της διαγωνίου ενός ορθογώνιου παραλληλεπιπέδου, μπορεί κανείς να γράψει

δηλαδή το μέτρο συντελεστή ενός διανύσματος είναι ίσο με την τετραγωνική ρίζα του αθροίσματος των τετραγώνων των προβολών του στους άξονες συντεταγμένων.

Έστω οι γωνίες του διανύσματος a με τους άξονες Ox, Oy και Oz, αντίστοιχα, ίσες με a, b, g. Με την ιδιότητα της προβολής του διανύσματος στον άξονα, έχουμε

Ή, τι είναι το ίδιο,

Οι αριθμοί ονομάζονται συνημίτονα κατεύθυνσης του διανύσματος α.

Αντικαθιστώντας τις εκφράσεις (5.5) με ισότητα (5.4), λαμβάνουμε

Μειώνοντας κατά παίρνουμε την αναλογία

δηλαδή, το άθροισμα των τετραγώνων των συνημιτόνων διεύθυνσης ενός μη μηδενικού διανύσματος είναι ίσο με ένα.

Είναι εύκολο να δούμε ότι οι συντεταγμένες του μοναδιαίου διανύσματος e είναι οι αριθμοί

Έτσι, λαμβάνοντας υπόψη τις συντεταγμένες ενός διανύσματος, μπορείτε πάντα να προσδιορίσετε το μέτρο και την κατεύθυνσή του, δηλ. το ίδιο το διάνυσμα.

Αλγεβρική διανυσματική προβολήσε οποιονδήποτε άξονα είναι ίσο με το γινόμενο του μήκους του διανύσματος και του συνημιτόνου της γωνίας μεταξύ του άξονα και του διανύσματος:

Δεξιά a b = |b|cos(a,b) ή

Όπου a b είναι το βαθμωτό γινόμενο των διανυσμάτων , |a| - μέτρο του διανύσματος a .

Εντολή. Για να βρείτε online την προβολή του διανύσματος Пp a b, πρέπει να καθορίσετε τις συντεταγμένες των διανυσμάτων a και b . Στην περίπτωση αυτή, το διάνυσμα μπορεί να δοθεί στο επίπεδο (δύο συντεταγμένες) και στο διάστημα (τρεις συντεταγμένες). Η λύση που προκύπτει αποθηκεύεται σε ένα αρχείο Word. Εάν τα διανύσματα δίνονται μέσω των συντεταγμένων των σημείων, τότε πρέπει να χρησιμοποιήσετε αυτήν την αριθμομηχανή.

Ταξινόμηση διανυσματικής προβολής

Τύποι προβολών εξ ορισμού διανυσματική προβολή

Η γεωμετρική προβολή του διανύσματος ΑΒ στον άξονα (διάνυσμα) ονομάζεται διάνυσμα Α"Β", αρχή του οποίου Α' είναι η προβολή της αρχής Α στον άξονα (διάνυσμα), και το άκρο Β' είναι η προβολή. του άκρου Β στον ίδιο άξονα.
Η αλγεβρική προβολή του διανύσματος ΑΒ στον άξονα (διάνυσμα) ονομάζεται μήκος του διανύσματος Α"Β", που λαμβάνεται με πρόσημο + ή -, ανάλογα με το αν το διάνυσμα Α"Β" έχει την ίδια διεύθυνση με τον άξονα ( διάνυσμα).

Τύποι προβολών κατά σύστημα συντεταγμένων

Διανυσματικές ιδιότητες προβολής

Η γεωμετρική προβολή ενός διανύσματος είναι διάνυσμα (έχει διεύθυνση).
Η αλγεβρική προβολή ενός διανύσματος είναι ένας αριθμός.

Διανυσματικά θεωρήματα προβολής

Θεώρημα 1. Η προβολή του αθροίσματος των διανυσμάτων σε οποιονδήποτε άξονα είναι ίση με την προβολή των όρων των διανυσμάτων στον ίδιο άξονα.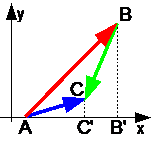

AC"=AB"+B"C"

Θεώρημα 2. Η αλγεβρική προβολή ενός διανύσματος σε οποιονδήποτε άξονα είναι ίση με το γινόμενο του μήκους του διανύσματος και του συνημιτόνου της γωνίας μεταξύ του άξονα και του διανύσματος:

Pr a b = |b| cos(a,b)

Τύποι διανυσματικών προβολών

προβολή στον άξονα OX.
προβολή στον άξονα OY.
προβολή σε ένα διάνυσμα.

Προβολή στον άξονα OX	Προβολή στον άξονα OY	Προβολή στο διάνυσμα
Αν η φορά του διανύσματος Α'Β' συμπίπτει με την κατεύθυνση του άξονα ΟΧ, τότε η προβολή του διανύσματος Α'Β' έχει θετικό πρόσημο.	Αν η φορά του διανύσματος Α'Β' συμπίπτει με την κατεύθυνση του άξονα ΟΥ, τότε η προβολή του διανύσματος Α'Β' έχει θετικό πρόσημο.	Αν η φορά του διανύσματος Α'Β' συμπίπτει με τη φορά του διανύσματος ΝΜ, τότε η προβολή του διανύσματος Α'Β' έχει θετικό πρόσημο.
Αν η φορά του διανύσματος είναι αντίθετη από την κατεύθυνση του άξονα ΟΧ, τότε η προβολή του διανύσματος Α'Β' έχει αρνητικό πρόσημο.	Αν η φορά του διανύσματος Α'Β' είναι αντίθετη από την κατεύθυνση του άξονα ΟΥ, τότε η προβολή του διανύσματος Α'Β' έχει αρνητικό πρόσημο.	Αν η φορά του διανύσματος Α'Β' είναι αντίθετη από τη φορά του διανύσματος ΝΜ, τότε η προβολή του διανύσματος Α'Β' έχει αρνητικό πρόσημο.
Αν το διάνυσμα ΑΒ είναι παράλληλο με τον άξονα ΟΧ, τότε η προβολή του διανύσματος Α'Β' ισούται με το μέτρο του διανύσματος ΑΒ.	Αν το διάνυσμα ΑΒ είναι παράλληλο με τον άξονα ΟΥ, τότε η προβολή του διανύσματος Α'Β' ισούται με το μέτρο του διανύσματος ΑΒ.	Αν το διάνυσμα ΑΒ είναι παράλληλο με το διάνυσμα ΝΜ, τότε η προβολή του διανύσματος Α'Β' είναι ίση με το μέτρο του διανύσματος ΑΒ.
Αν το διάνυσμα ΑΒ είναι κάθετο στον άξονα ΟΧ, τότε η προβολή του Α'Β' ισούται με μηδέν (μηδέν-διάνυσμα).	Αν το διάνυσμα ΑΒ είναι κάθετο στον άξονα ΟΥ, τότε η προβολή του Α'Β' ισούται με μηδέν (μηδενικό διάνυσμα).	Αν το διάνυσμα ΑΒ είναι κάθετο στο διάνυσμα ΝΜ, τότε η προβολή του Α'Β' είναι ίση με μηδέν (μηδενικό διάνυσμα).

1. Ερώτηση: Μπορεί η προβολή ενός διανύσματος να έχει αρνητικό πρόσημο. Απάντηση: Ναι, οι διανυσματικές προβολές μπορεί να είναι αρνητικές. Σε αυτήν την περίπτωση, το διάνυσμα έχει την αντίθετη κατεύθυνση (δείτε πώς κατευθύνονται ο άξονας OX και το διάνυσμα ΑΒ)
2. Ερώτηση: Μπορεί η προβολή ενός διανύσματος να συμπέσει με το μέτρο του διανύσματος. Απάντηση: Ναι, μπορεί. Στην περίπτωση αυτή, τα διανύσματα είναι παράλληλα (ή βρίσκονται στην ίδια ευθεία).
3. Ερώτηση: Μπορεί η προβολή ενός διανύσματος να είναι ίση με μηδέν (μηδέν-διάνυσμα). Απάντηση: Ναι, μπορεί. Στην περίπτωση αυτή, το διάνυσμα είναι κάθετο στον αντίστοιχο άξονα (διάνυσμα).

Παράδειγμα 1 . Το διάνυσμα (Εικ. 1) σχηματίζει γωνία 60 ο με τον άξονα ΟΧ (δίνεται από το διάνυσμα α). Εάν η ΟΕ είναι μονάδα κλίμακας, τότε |b|=4, άρα .

Πράγματι, το μήκος του διανύσματος (γεωμετρική προβολή b) είναι ίσο με 2, και η κατεύθυνση συμπίπτει με την κατεύθυνση του άξονα OX.

Παράδειγμα 2 . Το διάνυσμα (Εικ. 2) σχηματίζει γωνία με τον άξονα OX (με το διάνυσμα a) (a,b) = 120 o . Μήκος |b| Το διάνυσμα b είναι ίσο με 4, άρα pr a b=4 cos120 o = -2.

Πράγματι, το μήκος του διανύσματος είναι ίσο με 2 και η κατεύθυνση είναι αντίθετη από την κατεύθυνση του άξονα.