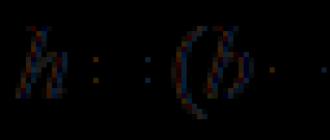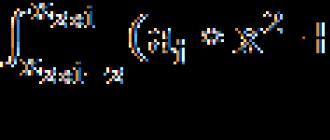Τι γίνεται αν υπάρχει ένα μείον μπροστά από τη μονάδα. Επίλυση εξισώσεων με μια ενότητα. Σεβασμός της ιδιωτικής ζωής σας σε επίπεδο εταιρείας
Η ενότητα αριθμών εισάγει μια νέα έννοια στα μαθηματικά. Ας ρίξουμε μια πιο προσεκτική ματιά στο τι είναι μια ενότητα αριθμών και πώς να συνεργαστεί με αυτήν;
Ας εξετάσουμε ένα παράδειγμα:
Βγήκαμε από το σπίτι στο μαγαζί. Περπατήσαμε 300 μέτρα, μαθηματικά, αυτή η έκφραση μπορεί να γραφτεί ως +300, η έννοια του αριθμού 300 από το σύμβολο " +" δεν θα αλλάξει. Η απόσταση ή το μέτρο ενός αριθμού στα μαθηματικά είναι ένα και το ίδιο μπορεί να γραφτεί ως εξής: | 300 | = 300. Το μέτρο ενός αριθμού υποδεικνύεται με δύο κάθετες γραμμές.
Και μετά περπατήσαμε 200 μέτρα προς την αντίθετη κατεύθυνση. Μαθηματικά, μπορούμε να γράψουμε τη διαδρομή επιστροφής ως -200. Αλλά δεν λέμε ότι "έχουμε περάσει μείον διακόσια μέτρα", αν και έχουμε επιστρέψει, επειδή η απόσταση ως τιμή παραμένει θετική. Για αυτό, η έννοια μιας ενότητας εισήχθη στα μαθηματικά. Μπορείτε να γράψετε την απόσταση ή το μέτρο του αριθμού -200 ως εξής: | -200 | = 200.
Ιδιότητες μονάδας.
Ορισμός:
Μέτρο ενός αριθμού ή απόλυτη τιμή ενός αριθμούΕίναι η απόσταση από το σημείο εκκίνησης έως το σημείο προορισμού.
Το μέτρο ενός μη μηδενικού ακέραιου αριθμού, πάντα θετικού αριθμού.
Η ενότητα γράφεται ως εξής:
1. Η απόλυτη τιμή ενός θετικού αριθμού είναι ίση με τον ίδιο τον αριθμό.
|
α | =ένα
2. Η απόλυτη τιμή ενός αρνητικού αριθμού είναι ίση με τον αντίθετο αριθμό.
|-
α | =ένα
3. Το συντελεστή μηδέν είναι μηδέν.
|0|=0
4. Οι ενότητες των αντίθετων αριθμών είναι ίσες.
|
a | = | -α | =ένα
Ερωτήσεις σχετικά με το θέμα:
Ποιο είναι το μέτρο ενός αριθμού;
Απάντηση: Η ενότητα είναι η απόσταση από το σημείο εκκίνησης έως το σημείο προορισμού.
Αν βάλετε ένα "+" μπροστά από έναν ακέραιο, τι συμβαίνει;
Απάντηση: ο αριθμός δεν θα αλλάξει τη σημασία του, για παράδειγμα, 4 = + 4.
Αν βάλετε ένα "-" μπροστά από έναν ακέραιο, τι συμβαίνει;
Απάντηση: Ο αριθμός θα αλλάξει σε, για παράδειγμα, 4 και -4.
Ποιοι αριθμοί έχουν το ίδιο μέτρο;
Απάντηση: οι θετικοί αριθμοί και το μηδέν θα έχουν το ίδιο μέτρο. Για παράδειγμα, 15 = | 15 |.
Ποιοι αριθμοί έχουν το αντίθετο συντελεστή;
Απάντηση: για αρνητικούς αριθμούς, το μέτρο θα είναι ίσο με τον αντίθετο αριθμό. Για παράδειγμα, | -6 | = 6.
Παράδειγμα # 1:
Βρείτε τη μονάδα αριθμών: α) 0 β) 5 γ) -7;
Λύση:
α) | 0 | = 0
β) | 5 | = 5
γ) | -7 | = 7
Παράδειγμα # 2:
Υπάρχουν δύο διαφορετικοί αριθμοί των οποίων οι απόλυτες τιμές είναι ίσες;
Λύση:
|10|=10
|-10|=10
Οι μονάδες αντίθετων αριθμών είναι ίσες.
Παράδειγμα # 3:
Ποιοι είναι οι δύο αντίθετοι αριθμοί που έχουν συντελεστή 9;
Λύση:
|9|=9
|-9|=9
Απάντηση: 9 και -9.
Παράδειγμα # 4:
Ακολουθήστε τα βήματα: α) | +5 | + | -3 | β) | -3 | + | -8 | γ) | +4 | - | +1 |
Λύση:
α) | +5 | + | -3 | = 5 + 3 = 8
β) | -3 | + | -8 | = 3 + 8 = 11
γ) | +4 | - | +1 | = 4 - 1 = 3
Παράδειγμα # 5:
Βρείτε: α) μέτρο αριθμού 2 β) μέτρο αριθμού 6 γ) μέτρο αριθμού 8 δ) μέτρο αριθμού 1 ε) μέτρο αριθμού 0.
Λύση:
α) το μέτρο του αριθμού 2 συμβολίζεται ως | 2 | ή | +2 | Αυτό είναι το ίδιο.
|2|=2
β) το μέτρο του αριθμού 6 συμβολίζεται ως | 6 | ή | +6 | Αυτό είναι το ίδιο.
|6|=6
γ) το μέτρο του αριθμού 8 συμβολίζεται ως | 8 | ή | +8 | Αυτό είναι το ίδιο.
|8|=8
δ) το μέτρο του αριθμού 1 συμβολίζεται ως | 1 | ή | +1 | Αυτό είναι το ίδιο.
|1|=1
ε) το μέτρο του αριθμού 0 συμβολίζεται ως | 0 |, | +0 | ή | -0 | Αυτό είναι το ίδιο.
|0|=0
Και υπολογίζεται σύμφωνα με τους ακόλουθους κανόνες:
Για συντομία, χρησιμοποιήστε | α |... Έτσι, | 10 | = 10; - 1/3 = | 1/3 | | -100 | = 100, κλπ.
Οποιοδήποτε μέγεθος NSαντιστοιχεί σε μια αρκετά ακριβή τιμή | NS|. Και αυτό σημαίνει Ταυτότητα στο= |NS| σκηνικά στοόπως μερικοί συνάρτηση επιχειρημάτων NS.
ΠρόγραμμαΑυτό λειτουργίαπαρουσιάζεται παρακάτω.
Για Χ > 0 |Χ| = Χ, και για Χ< 0 |Χ|= -Χ? από την άποψη αυτή, η γραμμή y = | Χ| στο Χ> 0 σε συνδυασμό με ευθεία γραμμή y = x(διχοτόμος της πρώτης γωνίας συντεταγμένων), και για NS< 0 - с прямой y = -x(διχοτόμος της δεύτερης γωνίας συντεταγμένων).
Επιλεγμένο εξισώσειςπεριλαμβάνει άγνωστους κάτω από την πινακίδα μονάδα μέτρησης.
Αυθαίρετα παραδείγματα τέτοιων εξισώσεων - | NS— 1| = 2, |6 — 2NS| =3NS+ 1 κ.λπ.
Επίλυση εξισώσεωνπου περιέχει το άγνωστο κάτω από το σύμβολο μέτρου βασίζεται στο γεγονός ότι εάν η απόλυτη τιμή του άγνωστου αριθμού x είναι ίση με έναν θετικό αριθμό a, τότε αυτός ο αριθμός x είναι ίσος με είτε a ή -a.
Για παράδειγμα: αν | NS| = 10, τότε ή NS= 10, ή NS = -10.
Σκεφτείτε επίλυση μεμονωμένων εξισώσεων.
Ας αναλύσουμε τη λύση της εξίσωσης | NS- 1| = 2.
Ας επεκτείνουμε την ενότητατότε η διαφορά NS- 1 μπορεί να είναι ίσο με + 2, ή - 2. Εάν x - 1 = 2, τότε NS= 3; αν NS- 1 = - 2, λοιπόν NS= - 1. Κάνουμε μια αντικατάσταση και έχουμε ότι και οι δύο αυτές τιμές ικανοποιούν την εξίσωση.
Απάντηση.Αυτή η εξίσωση έχει δύο ρίζες: Χ 1 = 3, Χ 2 = - 1.
Ας αναλύσουμε λύση εξίσωσης | 6 — 2NS| = 3NS+ 1.
Μετά επέκταση μονάδαςπαίρνουμε: ή 6 - 2 NS= 3NS+ 1, ή 6 - 2 NS= - (3NS+ 1).
Στην πρώτη περίπτωση NS= 1, και στο δεύτερο NS= - 7.
Εξέταση.Στο NS= 1 |6 — 2NS| = |4| = 4, 3Χ+ 1 = 4; προκύπτει από το δικαστήριο, NS = 1 - ρίζαδεδομένος εξισώσεις.
Στο Χ = - 7 |6 — 2Χ| = |20| = 20, 3Χ+ 1 = - 20; από 20 ≠ -20, λοιπόν NS= - 7 δεν είναι ρίζα αυτής της εξίσωσης.
Απάντηση. Εχωεξισώσεις μονής ρίζας: NS = 1.
Εξισώσεις αυτού του τύπου μπορεί να είναι επίλυση και γραφικά.
Ας αποφασίσουμε λοιπόν για παράδειγμα, γραφικά εξίσωση | NS- 1| = 2.
Αρχικά, εκτελούμε την κατασκευή γραφικά λειτουργιών στο = |Χ- 1 |. Το πρώτο είναι να σχεδιάσετε ένα γράφημα της συνάρτησης στο=NS- 1:
Αυτό το κομμάτι του γραφικάπου βρίσκεται πάνω από τον άξονα NSδεν θα αλλάξουμε. Για εκείνη NS- 1> 0 και επομένως | NS-1|=NS-1.
Το τμήμα του γραφήματος που βρίσκεται κάτω από τον άξονα NS, θα απεικονίσουμε συμμετρικώςσχετικά με αυτόν τον άξονα. Αφού για αυτό το μέρος NS - 1 < 0 и соответственно |NS - 1|= - (NS - 1). Το αποτέλεσμα γραμμή(σταθερή γραμμή) και θέληση γράφημα συνάρτησης y = | NS—1|.
Αυτή η γραμμή θα περάσει με ευθεία στο= 2 σε δύο σημεία: Μ 1 με τετμημένη -1 και Μ 2 με τετμημένη 3. Και, κατά συνέπεια, η εξίσωση | NS- 1 | = 2 θα υπάρχουν δύο ρίζες: NS 1 = - 1, NS 2 = 3.
Επίλυση εξισώσεων και ανισοτήτων με συντελεστή μέτρησηςείναι συχνά δύσκολο. Ωστόσο, αν καταλαβαίνετε καλά τι είναι την απόλυτη τιμή ενός αριθμού, και πώς να επεκτείνετε σωστά τις εκφράσεις που περιέχουν ένα σύμβολο μέτρου, τότε η παρουσία στην εξίσωση την έκφραση κάτω από το σύμβολο της ενότητας, παύει να αποτελεί εμπόδιο στη λύση του.
Λίγο θεωρία. Κάθε αριθμός έχει δύο χαρακτηριστικά: την απόλυτη τιμή του αριθμού και το πρόσημό του.
Για παράδειγμα, ο αριθμός +5, ή μόλις 5 έχει ένα σύμβολο " +" και μια απόλυτη τιμή 5.
Ο αριθμός -5 έχει σύμβολο " -" και απόλυτη τιμή 5.
Οι απόλυτες τιμές των 5 και -5 είναι 5.
Η απόλυτη τιμή του αριθμού x ονομάζεται μέτρο του αριθμού και συμβολίζεται με | x |.
Όπως μπορούμε να δούμε, το μέτρο ενός αριθμού είναι ίσο με τον ίδιο τον αριθμό, εάν αυτός ο αριθμός είναι μεγαλύτερος ή ίσος με το μηδέν, και σε αυτόν τον αριθμό με το αντίθετο πρόσημο, εάν αυτός ο αριθμός είναι αρνητικός.
Το ίδιο ισχύει για τυχόν εκφράσεις που βρίσκονται κάτω από το πρόσημο της ενότητας.
Ο κανόνας επέκτασης ενότητας μοιάζει με αυτόν:
| f (x) | = f (x) αν f (x) ≥ 0, και
| f (x) | = - f (x) αν f (x)< 0
Για παράδειγμα | x-3 | = x-3 αν x-3≥0 και | x-3 | =-(x-3) = 3-x αν x-3<0.
Για να λύσετε μια εξίσωση που περιέχει μια έκφραση κάτω από το πρόσημο μέτρο, πρέπει πρώτα επεκτείνετε τη μονάδα σύμφωνα με τον κανόνα επέκτασης της μονάδας.
Τότε η εξίσωση ή η ανισότητα μας μεταμορφώνεται σε δύο διαφορετικές εξισώσεις που υπάρχουν σε δύο διαφορετικά αριθμητικά εύρη.
Υπάρχει μια εξίσωση σε ένα αριθμητικό διάστημα όπου η έκφραση κάτω από το πρόσημο μέτρησης είναι μη αρνητική.
Και η δεύτερη εξίσωση υπάρχει στο διάστημα στο οποίο η έκφραση κάτω από το πρόσημο μέτρησης είναι αρνητική.
Ας ρίξουμε μια ματιά σε ένα απλό παράδειγμα.
Ας λύσουμε την εξίσωση:
| x-3 | = -x 2 + 4x-3
1. Ας επεκτείνουμε την ενότητα.
| x-3 | = x-3 αν x-3≥0, δηλ. αν x≥3
| x-3 | =-(x-3) = 3-x αν x-3<0, т.е. если х<3
2. Έχουμε δύο αριθμητικά εύρη: x≥3 και x<3.
Εξετάστε σε ποιες εξισώσεις μετατρέπεται η αρχική εξίσωση σε κάθε διάστημα:
Α) Για x≥3 | x-3 | = x-3, και η εξίσωση μας έχει τη μορφή:
Προσοχή! Αυτή η εξίσωση υπάρχει μόνο στο διάστημα x≥3!
Ας επεκτείνουμε τις αγκύλες, θα δώσουμε παρόμοιους όρους:
και λύστε αυτήν την εξίσωση.
Αυτή η εξίσωση έχει ρίζες:
x 1 = 0, x 2 = 3
Προσοχή! αφού η εξίσωση x-3 = -x 2 + 4x-3 υπάρχει μόνο στο διάστημα x≥3, μας ενδιαφέρουν μόνο οι ρίζες που ανήκουν σε αυτό το διάστημα. Αυτή η συνθήκη πληρούται μόνο με x 2 = 3.
Β) Για x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
Προσοχή! Αυτή η εξίσωση υπάρχει μόνο στο διάστημα x<3!
Ας επεκτείνουμε τις παρενθέσεις και δίνουμε παρόμοιους όρους. Παίρνουμε την εξίσωση:
x 1 = 2, x 2 = 3
Προσοχή! αφού η εξίσωση 3-x = -x 2 + 4x-3 υπάρχει μόνο στο διάστημα x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.
Έτσι: από το πρώτο διάστημα παίρνουμε μόνο τη ρίζα x = 3, από τη δεύτερη - τη ρίζα x = 2.
Ένα από τα πιο δύσκολα θέματα για τους μαθητές είναι η επίλυση εξισώσεων που περιέχουν μια μεταβλητή κάτω από το πρόσημο συντελεστή. Ας το καταλάβουμε για αρχή, με τι συνδέεται αυτό; Γιατί, για παράδειγμα, οι τετραγωνικές εξισώσεις είναι κλικ σαν τα καρύδια για τα περισσότερα παιδιά και με τόσο πολύ περίπλοκη έννοια ως ενότητα, έχει τόσα πολλά προβλήματα;
Κατά τη γνώμη μου, όλες αυτές οι δυσκολίες συνδέονται με την έλλειψη σαφώς διατυπωμένων κανόνων για την επίλυση εξισώσεων με ένα μέτρο. Έτσι, λύνοντας μια τετραγωνική εξίσωση, ο μαθητής γνωρίζει με βεβαιότητα ότι πρέπει πρώτα να εφαρμόσει τον διακριτικό τύπο και στη συνέχεια τον τύπο για τις ρίζες της τετραγωνικής εξίσωσης. Τι γίνεται όμως αν υπάρχει μια ενότητα στην εξίσωση; Θα προσπαθήσουμε να περιγράψουμε με σαφήνεια το απαραίτητο σχέδιο δράσης για την περίπτωση που η εξίσωση περιέχει ένα άγνωστο κάτω από το πρόσημο συντελεστή. Ακολουθούν ορισμένα παραδείγματα για κάθε περίπτωση.
Αλλά πρώτα, ας θυμηθούμε ορισμός ενότητας... Έτσι, το μέτρο του αριθμού έναο ίδιος ο αριθμός καλείται εάν έναμη αρνητικά και -ένααν ο αριθμός έναλιγότερο από το μηδέν. Μπορείτε να το γράψετε ως εξής:
| α | = a αν a ≥ 0 και | a | = -α αν α< 0
Μιλώντας για τη γεωμετρική αίσθηση της ενότητας, πρέπει να θυμόμαστε ότι κάθε πραγματικός αριθμός αντιστοιχεί σε ένα συγκεκριμένο σημείο στον αριθμητικό άξονα - το k του 
συντεταγμένη. Άρα, το μέτρο ή η απόλυτη τιμή ενός αριθμού είναι η απόσταση από αυτό το σημείο στην αρχή του αριθμητικού άξονα. Η απόσταση καθορίζεται πάντα ως θετικός αριθμός. Έτσι, η απόλυτη τιμή οποιουδήποτε αρνητικού αριθμού είναι θετικός αριθμός. Παρεμπιπτόντως, ακόμη και σε αυτό το στάδιο, πολλοί μαθητές αρχίζουν να μπερδεύονται. Οποιοσδήποτε αριθμός μπορεί να υπάρχει στη μονάδα, αλλά το αποτέλεσμα της εφαρμογής της ενότητας είναι πάντα ένας θετικός αριθμός.
Τώρα ας πάμε κατευθείαν στην επίλυση των εξισώσεων.
1. Εξετάστε μια εξίσωση της μορφής | x | = c, όπου c είναι πραγματικός αριθμός. Αυτή η εξίσωση μπορεί να λυθεί χρησιμοποιώντας τον ορισμό συντελεστή.
Χωρίζουμε όλους τους πραγματικούς αριθμούς σε τρεις ομάδες: αυτούς που είναι μεγαλύτεροι από μηδέν, αυτοί που είναι μικρότεροι από το μηδέν και η τρίτη ομάδα είναι ο αριθμός 0. Ας γράψουμε τη λύση με τη μορφή διαγράμματος:
(± c αν c> 0
Αν | x | = c, τότε x = (0, αν c = 0
(χωρίς ρίζες αν με< 0
1) | x | = 5, γιατί 5> 0, τότε x = ± 5;
2) | x | = -5, γιατί -5< 0, то уравнение не имеет корней;
3) | x | = 0, τότε x = 0.
2. Εξίσωση της μορφής | f (x) | = b, όπου b> 0. Για να λυθεί αυτή η εξίσωση, είναι απαραίτητο να απαλλαγούμε από το μέτρο. Το κάνουμε έτσι: f (x) = b ή f (x) = -b. Τώρα είναι απαραίτητο να λύσουμε κάθε μία από τις εξισώσεις που λαμβάνονται ξεχωριστά. Αν στην αρχική εξίσωση β< 0, решений не будет.
1) | x + 2 | = 4, γιατί 4> 0, λοιπόν
x + 2 = 4 ή x + 2 = -4
2) | x 2 - 5 | = 11, γιατί 11> 0, λοιπόν
x 2 - 5 = 11 ή x 2 - 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 χωρίς ρίζες
3) | x 2 - 5x | = -8, γιατί -οκτώ< 0, то уравнение не имеет корней.
3. Εξίσωση της μορφής | f (x) | = g (x) Κατά την έννοια της ενότητας, μια τέτοια εξίσωση θα έχει λύσεις εάν η δεξιά της πλευρά είναι μεγαλύτερη ή ίση με το μηδέν, δηλ. g (x) ≥ 0. Τότε θα έχουμε:
f (x) = g (x)ή f (x) = -g (x).
1) | 2x - 1 | = 5x - 10. Αυτή η εξίσωση θα έχει ρίζες αν 5x - 10 ≥ 0. Με αυτό ξεκινά η λύση τέτοιων εξισώσεων.
1. Ο.Δ.Ζ. 5x - 10 ≥ 0
2. Λύση:
2x - 1 = 5x - 10 ή 2x - 1 = - (5x - 10)
3. Ενώνουμε το ODZ. και η λύση, παίρνουμε:
Η ρίζα x = 11/7 δεν ταιριάζει σύμφωνα με το O.D.Z., είναι μικρότερη από 2 και το x = 3 πληροί αυτήν την προϋπόθεση.
Απάντηση: x = 3
2) | x - 1 | = 1 - x 2.
1. Ο.Δ.Ζ. 1 - x 2 ≥ 0. Λύνουμε αυτήν την ανισότητα με τη μέθοδο των διαστημάτων:
(1 - x) (1 + x) 0
2. Λύση:
x - 1 = 1 - x 2 ή x - 1 = - (1 - x 2)
x 2 + x - 2 = 0 x 2 - x = 0
x = -2 ή x = 1 x = 0 ή x = 1
3. Συνδυάζουμε το διάλυμα και το ODZ:
Μόνο οι ρίζες x = 1 και x = 0 είναι κατάλληλες.
Απάντηση: x = 0, x = 1.
4. Εξίσωση της μορφής | f (x) | = | g (x) |. Μια τέτοια εξίσωση ισοδυναμεί με τις ακόλουθες δύο εξισώσεις f (x) = g (x) ή f (x) = -g (x).
1) | x 2 - 5x + 7 | = | 2x - 5 |. Αυτή η εξίσωση είναι ισοδύναμη με τις ακόλουθες δύο:
x 2 - 5x + 7 = 2x - 5 ή x 2 - 5x +7 = -2x + 5
x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0
x = 3 ή x = 4 x = 2 ή x = 1
Απάντηση: x = 1, x = 2, x = 3, x = 4.
5. Εξισώσεις που επιλύονται με τη μέθοδο υποκατάστασης (μεταβλητή μεταβολή). Αυτή η μέθοδος λύσης είναι πιο εύκολο να εξηγηθεί με ένα συγκεκριμένο παράδειγμα. Έτσι, ας δοθεί μια τετραγωνική εξίσωση με ένα συντελεστή:
x 2 - 6 | x | + 5 = 0. Με την ιδιότητα της μονάδας x 2 = | x | 2, οπότε η εξίσωση μπορεί να ξαναγραφεί ως εξής:
| x | 2 - 6 | x | + 5 = 0. Ας αντικαταστήσουμε το | x | = t ≥ 0, τότε θα έχουμε:
t 2 - 6t + 5 = 0. Λύνοντας αυτήν την εξίσωση, παίρνουμε ότι t = 1 ή t = 5. Ας επιστρέψουμε στην αντικατάσταση:
| x | = 1 ή | x | = 5
x = ± 1 x = ± 5
Απάντηση: x = -5, x = -1, x = 1, x = 5.
Ας πάρουμε ένα άλλο παράδειγμα:
x 2 + | x | - 2 = 0. Με την ιδιότητα της μονάδας x 2 = | x | 2, επομένως
| x | 2 + | x | - 2 = 0. Ας αντικαταστήσουμε το | x | = t ≥ 0, τότε:
t 2 + t - 2 = 0. Λύνοντας αυτήν την εξίσωση, παίρνουμε t = -2 ή t = 1. Ας επιστρέψουμε στην αντικατάσταση:
| x | = -2 ή | x | = 1
Χωρίς ρίζες x = ± 1
Απάντηση: x = -1, x = 1.
6. Ένας άλλος τύπος εξισώσεων είναι οι εξισώσεις με ένα «σύνθετο» συντελεστή. Αυτές οι εξισώσεις περιλαμβάνουν εξισώσεις που έχουν "modules in a module". Οι εξισώσεις αυτού του είδους μπορούν να λυθούν χρησιμοποιώντας τις ιδιότητες της μονάδας.
1) | 3 - | x || = 4. Θα προχωρήσουμε με τον ίδιο τρόπο όπως και στις εξισώσεις του δεύτερου τύπου. Επειδή 4> 0, τότε παίρνουμε δύο εξισώσεις:
3 - | x | = 4 ή 3 - | x | = -4.
Τώρα εκφράζουμε σε κάθε εξίσωση το μέτρο x, τότε | x | = -1 ή | x | = 7.
Λύνουμε καθεμία από τις εξισώσεις που λαμβάνονται. Δεν υπάρχουν ρίζες στην πρώτη εξίσωση, γιατί -1< 0, а во втором x = ±7.
Η απάντηση είναι x = -7, x = 7.
2) | 3 + | x + 1 || = 5. Λύνουμε αυτήν την εξίσωση με τον ίδιο τρόπο:
3 + | x + 1 | = 5 ή 3 + | x + 1 | = -5
| x + 1 | = 2 | x + 1 | = -8
x + 1 = 2 ή x + 1 = -2. Χωρίς ρίζες.
Απάντηση: x = -3, x = 1.
Υπάρχει επίσης μια καθολική μέθοδος για την επίλυση εξισώσεων με ένα μέτρο. Αυτή είναι η μέθοδος της απόστασης. Αλλά θα το εξετάσουμε αργότερα.
ιστοτόπος ιστολογίου, με πλήρη ή μερική αντιγραφή του υλικού, απαιτείται σύνδεσμος προς την πηγή.
Δεν επιλέγουμε μαθηματικάτο επάγγελμά της και μας επιλέγει.
Ρώσος μαθηματικός Yu.I. Μάνιν
Εξισώσεις με συντελεστή
Τα πιο δύσκολα λύσιμα προβλήματα των σχολικών μαθηματικών είναι οι εξισώσεις που περιέχουν μεταβλητές κάτω από το πρόσημο συντελεστή. Για να επιλύσετε επιτυχώς τέτοιες εξισώσεις, πρέπει να γνωρίζετε τον ορισμό και τις βασικές ιδιότητες της ενότητας. Φυσικά, οι μαθητές πρέπει να έχουν τις δεξιότητες να λύσουν εξισώσεις αυτού του τύπου.
Βασικές έννοιες και ιδιότητες
Μέτρο (απόλυτη τιμή) πραγματικού αριθμούσυμβολίζεται και ορίζεται ως εξής:
Οι απλές ιδιότητες μιας μονάδας περιλαμβάνουν τις ακόλουθες αναλογίες:
Σημείωση, ότι οι δύο τελευταίες ιδιότητες ισχύουν για οποιοδήποτε ζυγό βαθμό.
Επιπλέον, αν, πού, τότε
Πιο πολύπλοκες ιδιότητες μονάδας, που μπορεί να χρησιμοποιηθεί αποτελεσματικά για την επίλυση εξισώσεων με μονάδες, διατυπώνονται με τα ακόλουθα θεωρήματα:
Θεώρημα 1.Για τυχόν αναλυτικές λειτουργίεςκαι η ανισοτητα ειναι αληθεια
Θεώρημα 2.Η ισότητα ισοδυναμεί με ανισότητα.
Θεώρημα 3.Ισότητα ισοδυναμεί με ανισότητα.
Ας εξετάσουμε τυπικά παραδείγματα επίλυσης προβλημάτων με θέμα "Εξισώσεις, που περιέχουν μεταβλητές κάτω από το σύμβολο της ενότητας ».
Επίλυση εξισώσεων με συντελεστή
Η πιο κοινή μέθοδος στα σχολικά μαθηματικά για την επίλυση εξισώσεων με μια ενότητα είναι η μέθοδος, βασίζεται στην επέκταση των ενοτήτων. Αυτή η μέθοδος είναι ευέλικτη, Ωστόσο, σε γενικές γραμμές, η εφαρμογή του μπορεί να οδηγήσει σε πολύ δύσκολους υπολογισμούς. Από αυτή την άποψη, οι μαθητές πρέπει να γνωρίζουν άλλα, πιο αποτελεσματικές μεθόδους και τεχνικές για την επίλυση τέτοιων εξισώσεων. Συγκεκριμένα, πρέπει να έχετε δεξιότητες στην εφαρμογή θεωρημάτων, δίνεται σε αυτό το άρθρο.
Παράδειγμα 1.Λύστε την εξίσωση. (1)
Λύση. Η εξίσωση (1) θα λυθεί με την "κλασική" μέθοδο - τη μέθοδο επέκτασης των ενοτήτων. Για να γίνει αυτό, χωρίζουμε τον αριθμητικό άξοναπόντους και ανά διαστήματα και εξετάστε τρεις περιπτώσεις.
1. Εάν, τότε ,,, και η εξίσωση (1) παίρνει τη μορφή. Συνεπώς ακολουθεί. Ωστόσο, εδώ, επομένως, η τιμή που βρέθηκε δεν είναι η ρίζα της εξίσωσης (1).
2. Εάν, τότε από την εξίσωση (1) παίρνουμεή .
Από τότε ρίζα της εξίσωσης (1).
3. Εάν, τότε η εξίσωση (1) παίρνει τη μορφήή . Σημειώστε ότι.
Απάντηση:,.
Κατά την επίλυση των επόμενων εξισώσεων με μια ενότητα, θα χρησιμοποιήσουμε ενεργά τις ιδιότητες των ενοτήτων προκειμένου να αυξήσουμε την αποτελεσματικότητα της επίλυσης τέτοιων εξισώσεων.
Παράδειγμα 2.Λύστε την εξίσωση.
Λύση.Αφού και, τότε η εξίσωση συνεπάγεται... Από την άποψη αυτή ,,, και η εξίσωση παίρνει τη μορφή... Από αυτό παίρνουμε... Αλλά , Επομένως, η αρχική εξίσωση δεν έχει ρίζες.
Απάντηση: δεν υπάρχουν ρίζες.
Παράδειγμα 3.Λύστε την εξίσωση.
Λύση.Από τότε. Αν τότε, και η εξίσωση παίρνει τη μορφή.
Από εδώ φτάνουμε.
Παράδειγμα 4.Λύστε την εξίσωση.
Λύση.Ξαναγράφουμε την εξίσωση σε ισοδύναμη μορφή. (2)
Η εξίσωση που προκύπτει ανήκει σε εξισώσεις του τύπου.
Λαμβάνοντας υπόψη το Θεώρημα 2, μπορεί να υποστηριχθεί ότι η εξίσωση (2) ισοδυναμεί με ανισότητα. Από εδώ φτάνουμε.
Απάντηση:.
Παράδειγμα 5.Λύστε την εξίσωση.
Λύση. Αυτή η εξίσωση έχει τη μορφή... Να γιατί , σύμφωνα με το Θεώρημα 3, εδώ έχουμε την ανισότηταή .
Παράδειγμα 6.Λύστε την εξίσωση.
Λύση.Υποθετω πως. Επειδή , τότε η δεδομένη εξίσωση παίρνει τη μορφή τετραγωνικής εξίσωσης, (3)
όπου ... Δεδομένου ότι η εξίσωση (3) έχει μία θετική ρίζακαι μετά ... Ως εκ τούτου, έχουμε δύο ρίζες της αρχικής εξίσωσης:και .
Παράδειγμα 7. Λύστε την εξίσωση. (4)
Λύση. Από την εξίσωσηισοδυναμεί με συνδυασμό δύο εξισώσεων:και , τότε, κατά την επίλυση της εξίσωσης (4), είναι απαραίτητο να ληφθούν υπόψη δύο περιπτώσεις.
1. Εάν, τότε ή.
Από εδώ παίρνουμε και.
2. Εάν, τότε ή.
Από τότε.
Απάντηση:,,,,.
Παράδειγμα 8.Λύστε την εξίσωση . (5)
Λύση.Από τότε και μετά. Από αυτό και από την Εξ. (5) προκύπτει ότι και, δηλ. εδώ έχουμε το σύστημα των εξισώσεων
Ωστόσο, αυτό το σύστημα εξισώσεων είναι ασυνεπές.
Απάντηση: δεν υπάρχουν ρίζες.
Παράδειγμα 9. Λύστε την εξίσωση. (6)
Λύση.Αν δηλώσουμε, τότε και από την εξίσωση (6) λαμβάνουμε
Ή . (7)
Δεδομένου ότι η εξίσωση (7) έχει τη μορφή, αυτή η εξίσωση ισοδυναμεί με ανισότητα. Από εδώ φτάνουμε. Από τότε, τότε ή.
Απάντηση:.
Παράδειγμα 10.Λύστε την εξίσωση. (8)
Λύση.Σύμφωνα με το Θεώρημα 1, μπορούμε να γράψουμε
(9)
Λαμβάνοντας υπόψη την εξίσωση (8), συμπεραίνουμε ότι και οι δύο ανισότητες (9) μετατρέπονται σε ισότητες, δηλ. ισχύει το σύστημα των εξισώσεων
Ωστόσο, σύμφωνα με το Θεώρημα 3, το παραπάνω σύστημα εξισώσεων ισοδυναμεί με το σύστημα των ανισοτήτων
(10)
Λύνοντας το σύστημα των ανισοτήτων (10), λαμβάνουμε. Δεδομένου ότι το σύστημα των ανισοτήτων (10) είναι ισοδύναμο με την εξίσωση (8), η αρχική εξίσωση έχει μία μόνο ρίζα.
Απάντηση:.
Παράδειγμα 11. Λύστε την εξίσωση. (11)
Λύση.Έστω και, στη συνέχεια, η ισότητα προκύπτει από την εξίσωση (11).
Ως εκ τούτου, προκύπτει ότι και. Έτσι, εδώ έχουμε ένα σύστημα ανισοτήτων
Η λύση σε αυτό το σύστημα ανισοτήτων είναικαι .
Απάντηση:,.
Παράδειγμα 12.Λύστε την εξίσωση. (12)
Λύση. Η εξίσωση (12) θα λυθεί με τη μέθοδο της διαδοχικής επέκτασης των ενοτήτων. Για να το κάνετε αυτό, εξετάστε διάφορες περιπτώσεις.
1. Αν, τότε.
1.1. Αν, τότε και ,.
1.2. Αν τότε. Αλλά , Επομένως, στην περίπτωση αυτή, η εξίσωση (12) δεν έχει ρίζες.
2. Αν, τότε.
2.1. Αν, τότε και ,.
2.2. Αν, τότε και.
Απάντηση:,,,,,.
Παράδειγμα 13.Λύστε την εξίσωση. (13)
Λύση.Δεδομένου ότι η αριστερή πλευρά της εξίσωσης (13) είναι μη αρνητική, τότε και. Από την άποψη αυτή, και η εξίσωση (13)
παίρνει τη μορφή ή.
Είναι γνωστό ότι η εξίσωση ισοδυναμεί με το συνδυασμό δύο εξισώσεωνκαι , αποφασίζουμε τι θα πάρουμε, Επειδή , τότε η εξίσωση (13) έχει μία ρίζα.
Απάντηση:.
Παράδειγμα 14. Επίλυση συστήματος εξισώσεων (14)
Λύση.Από και, τότε και. Επομένως, από το σύστημα των εξισώσεων (14) λαμβάνουμε τέσσερα συστήματα εξισώσεων:
Οι ρίζες των παραπάνω συστημάτων εξισώσεων είναι οι ρίζες του συστήματος εξισώσεων (14).
Απάντηση: ,,,,,,,,.
Παράδειγμα 15. Επίλυση συστήματος εξισώσεων (15)
Λύση.Από τότε. Από αυτή την άποψη, από το σύστημα των εξισώσεων (15), λαμβάνουμε δύο συστήματα εξισώσεων
Οι ρίζες του πρώτου συστήματος εξισώσεων είναι και, και από το δεύτερο σύστημα εξισώσεων λαμβάνουμε και.
Απάντηση:,,,,.
Παράδειγμα 16. Επίλυση συστήματος εξισώσεων (16)
Λύση.Από την πρώτη εξίσωση του συστήματος (16) προκύπτει ότι.
Από τότε ... Εξετάστε τη δεύτερη εξίσωση του συστήματος. Στο βαθμό που, τότε , και η εξίσωση παίρνει τη μορφή, , ή .
Αν αντικαταστήσετε την τιμήστην πρώτη εξίσωση του συστήματος (16), τότε, ή.
Απάντηση:,.
Για μια βαθύτερη μελέτη των μεθόδων επίλυσης προβλημάτων, που σχετίζονται με την επίλυση εξισώσεων, που περιέχουν μεταβλητές κάτω από το σύμβολο της ενότητας, μπορείτε να προτείνετε σεμινάρια από τη λίστα των προτεινόμενων διαβάσεων.
1. Συλλογή προβλημάτων στα μαθηματικά για τους αιτούντες στα τεχνικά κολέγια / Εκδ. ΜΙ. Σκανάβι. - Μ .: Ειρήνη και Εκπαίδευση, 2013 .-- 608 σελ.
2. Suprun V.P. Μαθηματικά για μαθητές λυκείου: προβλήματα αυξημένης πολυπλοκότητας. - Μ .: CD "Librokom" / URSS, 2017 .-- 200 σελ.
3. Suprun V.P. Μαθηματικά για μαθητές λυκείου: μη τυποποιημένες μέθοδοι επίλυσης προβλημάτων. - Μ .: CD "Librokom" / URSS, 2017.- 296 σελ.
Έχετε ακόμα ερωτήσεις;
Για να λάβετε βοήθεια από έναν εκπαιδευτή - εγγραφείτε.
ιστοσελίδα, με πλήρη ή μερική αντιγραφή του υλικού, απαιτείται σύνδεσμος προς την πηγή.
